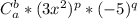, где p,q,a,b - целые(на самом деле, они все друг через друга выражаются, но это неважно). Независимо от значений переменных, этот одночлен будет содержать x в четной степени. Значит, среди всех слагаемых x^3 не будет, коэффициент при икс в кубе равен 0.
. Если раскрыть скобки второго сомножителя, то степени x будут только положительными, в частности, не будет одночлена, содержащего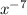 
. Значит, после домножения на первый сомножитель, увеличивающего все степени икс на 10, слагаемого с x^3 не будет. Коэффициент при икс в кубе равен 0.
В геометрической прогрессии
bn = b1 • q^(n-1)
В нашем случае
а)
b4 = b1 • q³
q³ = b4 / b1 = - 81/3 = - 27
q³ = - 27
q = - 3
ответ: - 3.
б)
b4 = b1 • q³
q³ = b4 / b1 = - 2/250 = - 1/125
q³ = - 1/125
q = - 1/5
ответ: - 1/5.