ответ:1)Алгебраической называют дробью.
2)Тождество — это уравнение, которое удовлетворяется тождественно
3)число n (показывающее сколько раз повторяется множитель) – показателем степени
4)Квадратное уравнение называют приведенным, если его старший коэффициент равен 1.
5)Решить уравнение - значит найти все его корни или установить, что их нет.
6)Деление числителя и знаменателя на их общий делитель, отличный от
единицы, называют сокращением дроби.
7)при умножении ( делении ) числителя и знаменателя на одно и то же выражение ( число) получившаяся дробь = исходной
8)числители перемножаются отдельно
отдельно знаменатели
полученную дробь если это возможно сокращают
пример
2/3* 3/4 = (2*3)/(3*4)=6/12=1/2 (произвели сокращение на 6
9)Вам известно, что значение обыкновенной дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число.
10) Сложение и вычитание алгебраических дробей c одинаковыми
знаменателями выполняется по тому же правилу, что и с обыкновенными
дробями:
аd + bd – cd = a+b−cd .
11) Нам известно, что дробь 34 равна частному 3 : 4 ,
значит, выражение ( 14+ 15) : ( 13− 16) = ( 14+ 15)( 13− 16) .
Частное двух чисел или выражений, в котором знак деления
обозначен чертой, называют дробным выражением.
Найдем значения выражений:
а) ( 14+ 15)( 13− 16) = ( 520+ 420)( 26− 16) = ( 920)( 16) = 920 : 16 =
= 920• 61 = 5420 = 2 710 = 2,7
12)Пусть a0 и a1 - натуральные числа. Для нахождения их наибольшего общего делителя используется алгоритм Евклида [1] последовательного деления с остатком: a0=a0a1+a2, a1=a1a2+a3, a2=a2a3+a4, … ,где натуральные числа a0,a1,a2, … суть неполные частные. Это алгоритм разложения числа a =a0/a1 в правильную цепную дробь, и он применим к любым вещественным числам a. При этомa0=[a], где [a] - целая часть числа a, a1=[1/(a-a0)], … , т.е.
a=a0+ 1a1+ 1a2+ 1a3+ ···,
13)http://school.xvatit.com/images/9/92/11-06-34.jpg
14)Складываются показатели степеней при УМНОЖЕНИИ степеней с одинаковыми основаниями.
2^3+2^5=8+32=40.
Подробнее - на -
Объяснение:
ответ: 1² - 2² + 3² - 4²+ 5² - 6²+ ... = (1-2)(1+2) + (3-4)(3+4)+ (5-6)(5+6) + ... =
= (-1) * (1+2+3+4+5+6+...+n) = (по формуле для арифметической прогрессии с разностью = 1 и числом членов = n) = (-1)*n*(n+1)/2 =
= -n(n+1)/2 - формула суммы для четного n.
Для нечетного n: S = (-1)* (1+2+3+...+ n-1) + n² = [То есть, к примеру, мы фиксируем сумму не на слагаемом типа -130², как в первом случае, а на слагаемом типа +131² и для данного места находим значение суммы ряда] = (-1)* (1+n-1)*(n-1)/2 + n² = -n(n-1)/2 + n² = (2n² - n² + n)/2 =
= (n²+n)/2 = n(n+1)/2.
В общем случае можно записать S(n) = [(-1)^(n-1)] * n(n+1)/2, n є N
Пусть стороны равны
и 
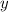. По условию:
Понятно, что система уравнений симметрична относительно переменных, поэтому: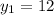
и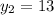 
(если непонятны рассуждения, найдите игреки по формуле 
).
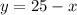ответ: 13 и 12 см.
Проверка:
Соответствует условию.
Что-нибудь непонятно? Спрашивай, с удовольствием объясню.