В решении.
Объяснение:
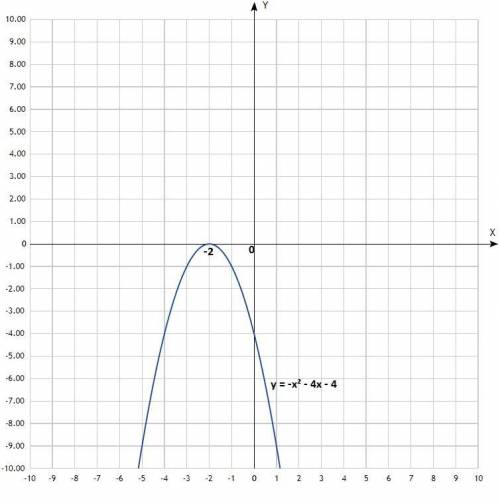
Постройте график функции у = -х2 – 4х – 4. Найти промежутки возрастания и убывания функции.
Дана функция у = -х² - 4х - 4;
Построить график.
График - парабола со смещённым центром, ветви направлены вниз.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = -х² - 4х - 4;
Таблица:
х -5 -4 -3 -2 -1 0 1
у -9 -4 -1 0 -1 -4 -9
По вычисленным точкам построить параболу.
Функция возрастает на промежутке х∈(-∞; -2).
Функция убывает на промежутке х∈(-2; +∞).
Объяснение:
йоу,чувак
Мы можем сложить эти два уравнения и получить вместо закорючек:косинусов и синусов - единицу.
Ведь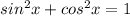
Т.е при сложении этих уравнений мы получим третье уравнение(да,мы просто сложим друг с другом почленно эти выражения, левая сторона с левой и правая сторона с правой).
Упс... чуть не забыл ОДЗ! Ведь нельзя забывать,что под корнем у нас могут находиться лишь неотрицательные числа(АУФ),но это пока мы не добрались до комплексного пространства,ну да ладно,оно сейчас не нужно. Итак составим неравенство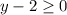
т.е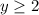
. Так-с... ОДЗ мы нашли. Вернёмся к истокам.
уравнение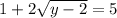
с одной переменной решается легко,всего-лишь щелчк... возведением в квадрат обеих частей уравнения!
Мы нашли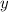
. И чему он равен? Правильно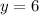 
теперь подставим данное значение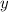
в эти уравнения.
И получим следующее
И всё!! Задача почти решена!
Предлагаю тебе обратиться к таблице синусов и косинусов и посмотреть, при каких значениях
синус обращается в нуль,а косинус в 1.
Удачи тебе, my dear!