Если я правильно поняла, то нужно заполнить поле y при определенном x. Так и поступим.
Подставляем на место x поочередно числа. Первое уравнение я напишу подробно.
y= -3.1 + (-8.9) x= -8.9
y= -3.1-8.9 (плюс на минус будет минус)
Если только начали работать с минусами то можно их вынести за скобку.
y= -(3,1+8,9)
y= -(12) = -12
При x= -8.9 y=-12
Идем далее. Все делаем по тому же принципу, расписывать я эти выражения не буду.
x=-2.4
y= -3.1+(-2.4)
y= -5.5 При x=-2.4 y=-5.5
x= 1.9
y=-3.1+1.9
y= 1.9-3.1(от перемены мест слагаемых значение суммы не меняется)
y=-1.2 x= 1.9
y= -3.1+7.6
y= 4.5 x=7.6
y=-3.1+12.9
y= 9.8 x= 12.9
Готово. Надеюсь правильно поняла задание. Пс. Это можно было решить и на калькуляторе)
1661
Объяснение:
По условию на доске написаны составные числа
a₁, a₂, ..., aₓ,
где aₓ ≤ 1700 и НОД(a₁, a₂)=...=НОД(a₁, aₓ)=НОД(a₂, a₃)=...=
=НОД(a₂, aₓ)=...=НОД(aₓ₋₁, aₓ) = 11.
Как известно, любое составное число А можно представить в виде разложения на простые множители
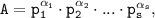
где 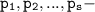 простые числа,
простые числа, 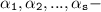 неотрицательные целые числа.
неотрицательные целые числа.
Так как наибольший общий делитель (НОД) любых двух чисел равен 11, то разложение каждого числа содержит множитель pₓ = 11 и αₓ = 1, а остальные простые множители любой пары различны. Отсюда, первое число, которого написал Олег - это 11. Далее, последовательность можно представить в виде
11·2, 11·3, 11·5, 11·7, 11·11, ..., 11·pₐ.
Из 11·pₐ ≤ 1700 находим pₐ:
11·pₐ ≤ 1700
pₐ ≤ 1700:11
pₐ ≤ 154 6/11.
Наибольшее простое число удовлетворяющее последнее неравенство - это 151. Тогда 11·151= 1661.
Заметим, что у нас должен получиться слева квадрат некоего числа. Значит и справа должен быть квадрат. Так как
При 25, получаем 31-ab=25, Из этого следует, что ab=6. Причем оба этих числа положительны.
С другой стороны
При 16, получаем 31-ab=16. Из этого следует, что ab=15. Получается пара чисел а=5, b=3, или наоборот. Но вот квадрат разности не даст желаемых 16. Другие пары здесь невозможны. 15 и 1 не подойдут.
При 9, получаем 31-ab=9. ab=22. Тут снова не выходит пара чисел. Так как 22=2*11. Эти числа не могут быть а и b. 22=1*22 - тоже не нужный вариант.
При 4, получаем 31-ab=4. ab=27. Тут получается пара чисел 9 и 3. Но вот квадрат их разности будет равен 36. А это не дает 4.
При 1, получаем ab=30. Пара допустимая будет a=5, b=6 или a=6, b=5. Здесь квадрат разности будет равен 1. То есть
Таким образом, перебрали все возможные варианты и пришли к 4 числам 16, 61, 56, 65.
Теперь вычислим их сумму: 16+61+65+56=77+121=198.
ответ: 198 - это сумма нужных нам двузначных чисел.