Решение на прикреплённой фотографии
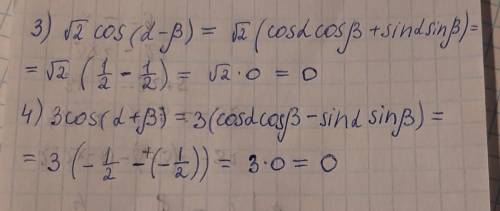
Объяснение:
чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?чего обычно начинается повествование?
Как развивалось событие дальше?
Что произошло однажды?
Чем закончилась сказка?
Оправдываешь ли ты действия героя?
-3.
Объяснение:
√(6 -2√5) - √(9+4√5) =
Заметтм, что каждое подкоренное выражение можно представить в виде квадрата суммы или разности:
6 -2√5 = 5 -2√5 + 1 = (√5)^2 -2•√5•1 + 1^2 =
(√5 -1)^2.
9 + 4√5 = 5 + 4√5 + 4 = (√5)^2 + 2•√5•2 + 2^2 =
(√5 + 2)^2.
Именно поэтому решение запишется так:
√(6 -2√5) - √(9+4√5) = √(√5 -1)^2 - √(√5 + 2)^2 = l√5 - 1l - l√5 + 2l
Выражения, записанные под знаком модуля положительные, знак модуля опускаем, не меняя знаки слагаемых в скобках:
(√5 - 1) - (√5 + 2) =
Упрощаем получившееся выражение:
√5 - 1 - √5 - 2 = -1 -2 = -3.
ответ: -3.
Использованные тождества:
а^2 - 2аb + b^2 = (a-b)^2;
а^2 + 2аb + b^2 = (a+b)^2;
√(a)^2 = lal.
V3)
Используя тригонометрическое тождество cos(a - b) = cos(a)cos(b) + sin(a)sin(b) и условие соsα соsß, получаем:
cos(a - b) = cos(a)cos(ß) + sin(a)sin(ß) = cos(α)cos(ß) + sin(α)sin(ß) = cos(α - ß)
Тогда √√2 cos(a - b) = √√2 cos(α - ß).
V4)
Используя тригонометрические тождества cos(a + b) = cos(a)cos(b) - sin(a)sin(b) и sin(2θ) = 2sin(θ)cos(θ), получаем:
3 cos(a + ß) = 3(cos(a)cos(ß) - sin(a)sin(ß)) = 3cos(a)cos(ß) - 3sin(a)sin(ß) = 3(cos(a)cos(ß) - sin(a)sin(ß))sin(α)sin(ß) / (sin(α)sin(ß))
= 3(sin(α)cos(ß) + cos(α)sin(ß))sin(α)sin(ß) / (sin(α)sin(ß)) = 3(sin^2(α)cos(ß) + cos^2(α)sin(ß)) = 3(sin^2(α) + cos^2(α))sin(ß) = 3sin(ß)
Таким образом, 3 cos(a + ß) = 3sin(ß)