Нужно использовать следующие свойства числовых неравенств:
1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:
если а < b и с - любое число, то a + c < b + c.
2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:
если а < b и с > 0, то ac < bc;
если а < b и с < 0, то ac >bc.
Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),
а затем и 2,5а - 7 < 2,5b - 7.
ответ: 2,5а - 7 < 2,5b - 7.
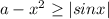
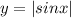расположен выше оси ОХ. 
.
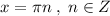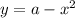- это параболы , ветви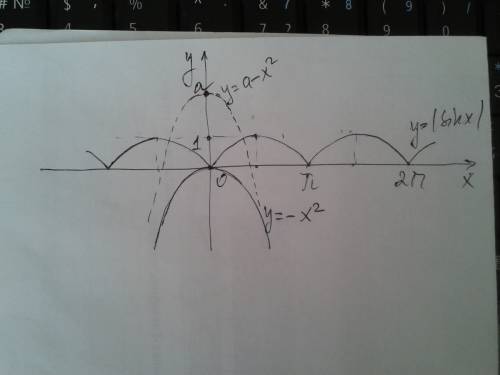
Рассмотрим треугольник АВС. У него угол А равен 27 градусов, В равен 98 градусов, значит АСВ равен 55 градусов (180-27-98=55). Рассмотрим треугольник ВКС. Так как ВК - бисектрисса, то угол СВК равен (98/2=49) 49 градусов. В треугольнике ВКС угол ВКС равен 76 градусов (180-49-55=76). Рассмотрим треугольник АМС. Поскольку АМ - бисектрисса угла ВАС, то угол МАС равен (27/2=14) 14 градусов. В треугольнике АСМ угол АМС равен (180-55-14=111) 111градусов. Рассмотрим четырехугольник VNRC/ Ранее выяснили, что угол АСВ равен 55 градусов, Угол АМС равен 111 градусов, угол ВКС равен 76 градусов. Так как сумма внутренних углов четырехугольника равна 360 градусов, то угол МТК равен 118 градусов (360-111-55-76=118).