В решении.
Объяснение:
91.
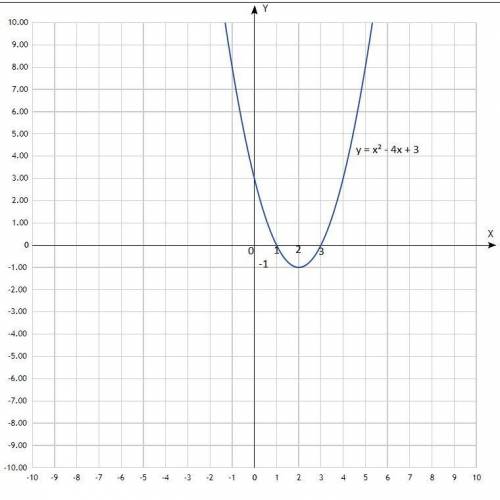
Построить график функции у = х² - 4х + 3;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -1 0 1 2 3 4 5
у 8 3 0 -1 0 3 8
По вычисленным точкам построить параболу.
Пользуясь графиком, определить:
1) у наим. и у наиб.;
у наиб. не существует;
у наим. = -1;
2) область значений функции;
Область значений Е(у) >= -1;
3) промежутки возрастания и убывания функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2);
4) решения неравенств f(x)>0; f(x)<=0.
f(x)>0 при х∈(-∞; 1)∪(3; +∞); парабола выше оси Ох;
f(x)<=0 при х[1; 3]; парабола ниже оси Ох.
92.
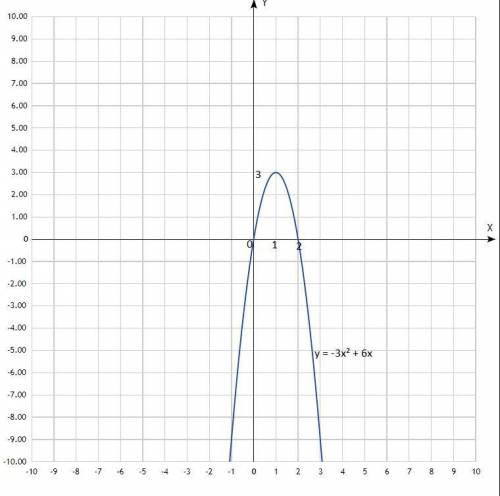
Построить график функции у = 6х - 3х²;
у = -3х² + 6х;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -1 0 1 2 3
у -9 0 3 0 -9
По вычисленным точкам построить параболу.
Пользуясь графиком, определить:
1) у наим. и у наиб.;
у наим. не существует;
у наиб. = 3;
2) область значений функции;
Область значений Е(у) <= 3;
3) промежутки возрастания и убывания функции;
Функция возрастает при х∈(-∞; 1);
Функция убывает при х∈(1; +∞);
4) решения неравенств f(x)>0; f(x)<=0.
f(x)>0 при х∈(0; 2); парабола выше оси Ох;
f(x)<=0 при х∈(-∞; 0]∪[2; +∞); парабола ниже оси Ох.
В решении.
Объяснение:
91.
Построить график функции у = х² - 4х + 3;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вверх.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -1 0 1 2 3 4 5
у 8 3 0 -1 0 3 8
По вычисленным точкам построить параболу.
Пользуясь графиком, определить:
1) у наим. и у наиб.;
у наиб. не существует;
у наим. = -1;
2) область значений функции;
Область значений Е(у) >= -1;
3) промежутки возрастания и убывания функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2);
4) решения неравенств f(x)>0; f(x)<=0.
f(x)>0 при х∈(-∞; 1)∪(3; +∞); парабола выше оси Ох;
f(x)<=0 при х[1; 3]; парабола ниже оси Ох.
92.
Построить график функции у = 6х - 3х²;
у = -3х² + 6х;
Уравнение квадратичной функции, график - парабола со смещённым центром, ветви направлены вниз.
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
Таблица:
х -1 0 1 2 3
у -9 0 3 0 -9
По вычисленным точкам построить параболу.
Пользуясь графиком, определить:
1) у наим. и у наиб.;
у наим. не существует;
у наиб. = 3;
2) область значений функции;
Область значений Е(у) <= 3;
3) промежутки возрастания и убывания функции;
Функция возрастает при х∈(-∞; 1);
Функция убывает при х∈(1; +∞);
4) решения неравенств f(x)>0; f(x)<=0.
f(x)>0 при х∈(0; 2); парабола выше оси Ох;
f(x)<=0 при х∈(-∞; 0]∪[2; +∞); парабола ниже оси Ох.


a1q³+q1q^4+a1q^5=a1q³(1+q+q²)=42⇒q³=42/a1(1+q+q²)=42/192=7/36
а)S(с 7 по 9)=a1q^6+a1q^7+a1q^8)=a1q^6(1+q+q²)=q³*a1q³(1+q+q²)=7/36*42=49/6
б)S(с 10 по 12)=a1q^9+a1q^10+a1q^11=a1q^9(1+q+q²)=q³*a1q^6(1+q+q²)=
=7/36*49/6=373/216
S(с 1 по 12)=S( c 1 по3)+S( c 4 по6)+S( c 7 по9)+S( c 10 по12)=
=192+42+49/6+343/216=234+1764/216+343/216=234+2107/216=
=234+9 163/216=243 163/216