1) (2x+1)=x+28
2x+1=x+28
2x+x=28-1
3x=27
x=27/3
x=9
5 не является корнем уровнения (2x-1)=x+28
x(x+3)=10
x+3x=10
x+3x=10
5 не является корнем x(x+3)=10
2) уровнение а) линейное
3) 42x=64
x=64/42
x= 1,5
-1,5x=9
x=9/(-1,5)
x=6
2 1/2x+15=30
2 1/2x=30-15
2 1/2=15
x=15/2 1/2
x=6
В решении.
Объяснение:
Первое задание.
Координаты точек пересечения графиком осей координат:
(-2; 0) и (0; -4)
Уравнение функции у = kx + b
Подставить в это уравнение первые известные значения х= -2 и у=0.
Получим первое уравнение системы:
k * (-2) + b = 0;
Подставить в это же уравнение вторые значения х= 0 и у= -4.
Получим второе уравнение системы:
k * 0 + b = -4
Решить систему:
k * (-2) + b = 0;
k * 0 + b = -4
Из второго уравнения b = -4, подставить в первое и вычислить k:
-2k - 4 = 0
-2k = 4
k = 4/-2
k = -2.
Подставить вычисленные значения k и b в уравнение у=kx + b и получить нужное уравнение:
у = -2х - 4.
Второе задание.
Координаты точек пересечения графиком осей координат:
(-4; 0) и (0; 2)
Уравнение функции у = kx + b
Подставить в это уравнение первые известные значения х= -4 и у=0.
Получим первое уравнение системы:
k * (-4) + b = 0;
Подставить в это же уравнение вторые значения х= 0 и у= 2.
Получим второе уравнение системы:
k * 0 + b = 2
Решить систему:
k * (-4) + b = 0;
k * 0 + b = 2
Из второго уравнения b = 2, подставить в первое и вычислить k:
-4k + 2 = 0
-4k = -2
k = -2/-4
k = 0,5.
Подставить вычисленные значения k и b в уравнение у=kx + b и получить нужное уравнение:
у = 0,5х + 2.
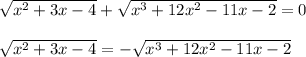

1.Не является ни под а), ни под б).
2.Линейное под а)
3.а) 42х=-64
х=-64/42= -одна целая 22/42=-одна целая 11/21
б) -1,5х=9
х=-6
в)Две целых 1/2*х+15=30
5/2*х=15
х=6