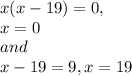
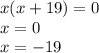
Домножим числитель и знаменатель на такое число, что бы получить в знаменателе квадрат целого числа. Проще всего домножить на 7:
28/49 и 35/49
Но между 28 и 35 нету квадратов целых чисел, поэтому надо ещё домножить числитель и знаменатель каждого числа, но уже на квадрат какого-то целого числа, например, на 4 ,9, 16 и т.д. Попробуем умножить на 4:
112/196 и 140/196
Между числами 112 и 140 есть число 121, которое является квадратом числа 11. Поэтому искомое число 121/196 (так как оно будет квадратом числа 11/14).
Можно калькулятором себя проверить, действительно ли число 121/196 будет находится между 4/7 и 5/7:
4/7 = 0,5714...
121/196 = 0,6173...
5/7 = 0,7143...
нет
Объяснение:
2x² +2x +1 -7y² = 2007 ⇔ 2x²+2x -2006 = 7y² ( 1 )
так как левая часть равенства ( 1 ) - четное число , то и правая
часть кратна 2 ⇒ 7y² делится на 2 ⇒ y делится на 2 ⇒
y = 2k ; k∈Z , подставим в (1) вместо y число 2к :
2x²+2x -2006 =28k² ⇒ x²+x -14k² = 1003 или :
x(x+1) -14k² = 1003 ( 2 )
x и ( x +1 ) - 2 последовательных натуральных числа ⇒ одно
из них обязательно четно ⇒ x(x+1) - четно ⇒ x(x+1) -14k² - четно
, как разность двух четных чисел , но 1003 - нечетное число
⇒ равенство ( 2) невозможно ⇒ уравнение (1) не имеет
решений в целых числах
х=0
х=19
х(х+19)=0
х=0
х=-19