(23/15)х t=s
где "с" пройденное расстояние
Объяснение:
ОДЗ x²+2x-8>0
решим неравенство методом интервалов
x² + 2x - 8 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 2²2 - 4·1·(-8) = 4 + 32 = 36
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = (-2 - √36)/ 2·1 = ( -2 - 6)/ 2 = -8 /2 = -4
x₂ = (-2 + √36 )/2·1 =( -2 + 6)/ 2 = 4/ 2 = 2
(-∞)(-4)2(+∞)
+ - +
x∈(-∞;-4)∪(2;+∞) - это ОДЗ
log₄(x²+2x-8)<2
x²+2x-8<4²
x²+2x-8<16
x²+2x-8-16<0
x²+2x-24<0
решим неравенство методом интервалов
x² + 2x - 24 = 0
Найдем дискриминант квадратного уравнения:
D = b² - 4ac = 2² - 4·1·(-24) = 4 + 96 = 100
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x₁ = ( -2 - √100 )/2·1 = ( -2 - 10)/ 2 = -12 /2 = -6
x₂= ( -2 + √100)/ 2·1 = ( -2 + 10)/ 2 = 8 / 2 = 4
(-∞)(-6)4(+∞)
+ - +
x∈(-6;4)
c учетом ОДЗ x∈(-∞;-4)∪(2;+∞)
x∈(-6;-4)∪(2;4)
выбираем целые значения
х={-5;3}
9.
Пусть x (км/ч) — скорость теплохода в стоячей воде
y (км/ч) — скорость течения
тогда скорость по течению (х+у) км/ч , против течения (х-у) км/ч
Составим уравнение :
3(x+y)+ 2(x-y) =240
3(x-y)-2(x+y )=35
—————————————
5x+y=240
x-5y=35
—————————————
x=35+5y
5(35+5y) +у=240
175 +25у+у=240
26у =65
у=2,5 км/ч скорость течения
х=35 +5*2,5 = 47,5 км/ч скорость теплохода в стоячей воде
47.5- 2.5 =45 км/ч скорость теплохода против течения
47.5 +2,5=50 км/ч скорость теплохода по течению.
остальные на листочке 7,8.
но 10 я так и не поняла совсем задание
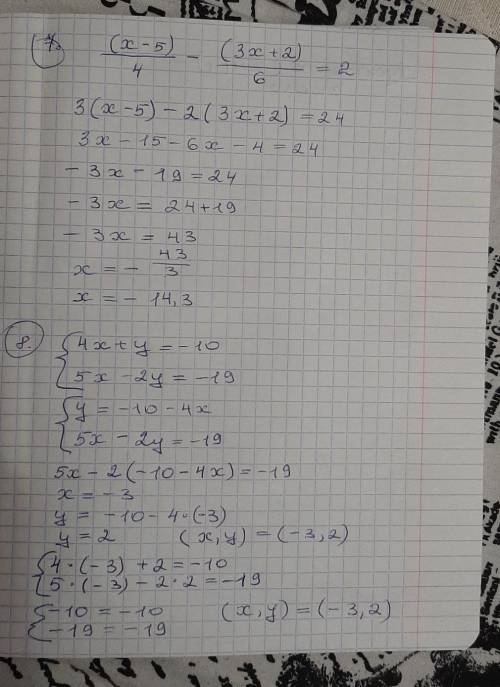
1) нужно найти скорость- 23:15
2) если скорость мы знаем и время тоже знаем, нужно найти расстояние - т.е. то, что получилось в пункте 1 умножаем на время(t)
я думаю так, сдесь же не нужен точный ответ, а только выражение