это картинка твоей задачи
давай я попытаюсь объяснить теорему косинусов (доказывать её не собираюсь, можешь посмотреть док-во в интернетах)
у нас есть треугольник со сторонами a,b,c, и угол между a и b равен альфа, тогда верно такое равенство:
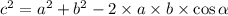
используем это чтобы найти сторону XY
пусть XY=x
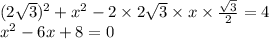
получаем
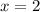
либо
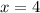
если мы рассмотрим первый случай, то у нас равнобедренный по определению треугольник, значит, по свойству равнобедренного треугольника, угол XZY=XYZ=30°
соответственно YXZ=180° - 2*30° = 120°
во втором случае мы снова расписываем формулу по теореме косинусов, где наш искомый угол равен бета
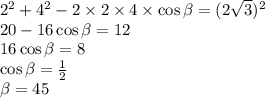
готово
непонятно - пиши
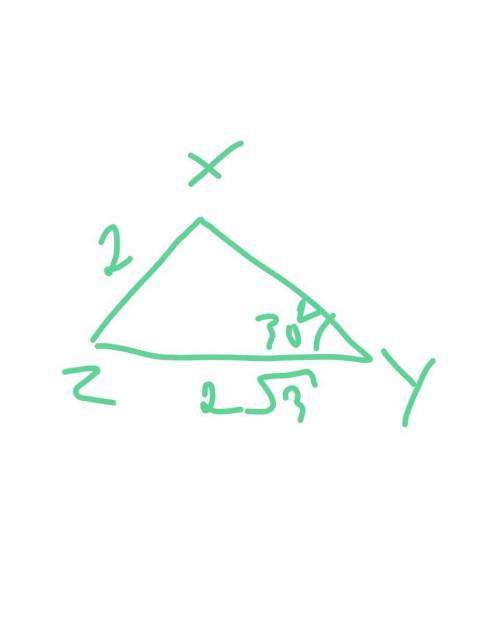
(-6, -5 )
Объяснение:
P.S забыла скобку фигурную слева, там где x = -2y-16, -5y=25
Если коротко объяснить решения, то это метод подстановки. Выражаем одну переменную через другую и подставляем ее в другое уравнение. Ещё можно решать через графический метод, но это достаточно долго, можно было привести через метод алгебраического сложения:
{x+2y=-16,
{2x-y=-7; | Будем действовать через игрек. Умножаем уравнение на 2.
{x+2y=-16,
{4x-2y=-14;
Теперь там где фигурная скобка ( она должна быть большой, захватывать два уравнения ), мы ставим знак + и складываем уравнения.
{x+2y=-16,
{4x-2y=-14;
_________
(x+4x)+(2y+(-2y))=-16+(-14)
2y у нас уходят, получаем:
5x=-30, | 5
x=-6.
Возвращаемся к системе уравнений, не забывая переписать x.
{x=-6,
{-6+2y=-16;
{x=-6,
{2y=-16+6;
{x=-6,
{2y=-10; | 2
{x=-6,
{y=-5.
И, собственно, получим тот же ответ. Алгебраическое сложение можно использовать и с минусом. ( если бы у нас вышло, например, x+2y=-16 и 4x+2y=-14. Тогда бы все, что поменялось, так это сложение мы бы заменили вычитанием.
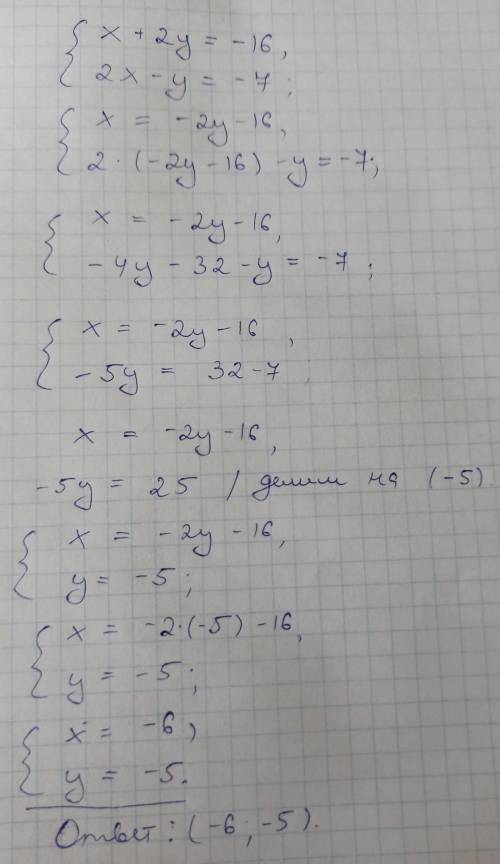
sinx > (√3)*cosx делим на cosx ≠ 0
tgx > √3
arctg(√3) + πn < x < π/2 + πn, n∈Z
π/3 + πn < x < π/2 + πn, n∈Z