Признак сходимости знакочередующихся рядов (признак Лейбница):
Пусть имеется ряд
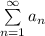
Тогда, если выполнены условия:
Ряд является знакочередующимся. Члены ряда убывают по модулю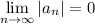
то ряд сходится.
1) Чередование знаков
Ряд является знакочередующимся, т.к. присутствует множитель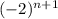 
2) Убывание по модулю
![\lim\limits_{n\to \infty}|\frac{(-2)^{n+1}}{2+3^n} |=\lim\limits_{n\to \infty}\frac{2^{n+1}}{2+3^n}=[\frac{\infty}{\infty} ]](/tpl/images/2004/2358/902ef.png)
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
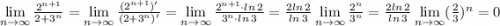
Таким образом, ряд сходится
Тип сходимости Сходящийся ряд 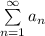называют абсолютно сходящимся, если сходится ряд 
.
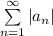Сходимость такого ряда можно определить с предельного признака Даламбера
![\lim\limits_{n\to \infty}\frac{|a_{n+1}|}{|a_n|} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}:\frac{2^{n+1}}{2+3^{n}} =\lim\limits_{n\to \infty}\frac{2^{n+2}}{2+3^{n+1}}\cdot\frac{2+3^{n}}{2^{n+1}} =2\lim\limits_{n\to \infty}\frac{2+3^{n}}{2+3^{n+1}}=[\frac{\infty}{\infty} ]](/tpl/images/2004/2358/41dfd.png)
Неопределенность вида "бесконечность делить на бесконечность" решим по правилу Лопиталя
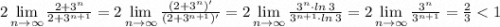
Ряд сходится по признаку Вейерштрасса, следовательно исходный ряд сходится абсолютно.
ответ: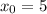 
.
Угловой коэффициент прямой у=2х-2 равен k=2 . Если касательная параллельна этой прямой или совпадает с ней , то их угловые коэффициенты равны.
Угловой коэффициент касательной к графику функции y=f(x) равен значению производной в точке касания, то есть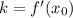 
.
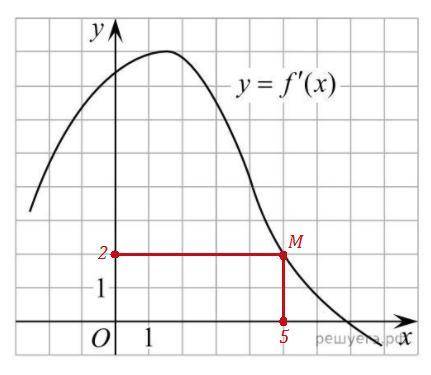
На оси ординат находим значение у=2, проводим прямую, параллельную оси ОХ, и находим на графике функции точку М - точку пересечения графика с прямой у=2.
Далее Находим абсциссу точки М . Это и будет абсцисса точки, в которой касательная к графику функции y=f(x) параллельна прямой y=2x-2 или совпадает с ней.
Координаты точки М(5;2) , значит .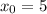
D=16-4*1*7<0
корней нет