Алгебра: F(x)=x3/3-1,5x2-4x f(x)=0 решить уравнение

F(x)=x3/3-1,5x2-4x f(x)=0 решить уравнение

👇

Увидеть ответ

Ответ:

irina20042005

21.08.2021

X³/3-1,5x²-4x=0
x(x²/3-1,5x-4)=0
x₁=0
x²-4,5x-12=0 D=145/4
x₂≈-1,88 x₃≈6,38.

4,8(46 оценок)

Открыть все ответы

Ответ:

9872105

21.08.2021

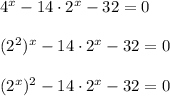
$4^x - 14\cdot 2^x - 32 = 0\\\\(2^2)^x - 14\cdot 2^x - 32 = 0\\\\(2^x)^2 - 14\cdot 2^x - 32 = 0$

Введём замену: 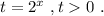$t = 2^x\ , t0\ .$

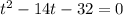
t^2 - 14t - 32 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -32\\t_{1} + t_{2} = 14\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 16; t = -2}$ .

Но так как 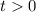t 0 , то -2 не является решением этого уравнения. Выполняем обратную замену:

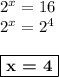
$2^x = 16\\2^x = 2^4\\\\\boxed{\textbf{x = 4}}$

ответ: 4.

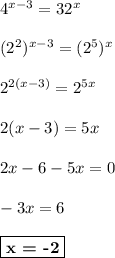
$4^{x-3} = 32^x\\\\(2^2)^{x-3} = (2^5)^x\\\\2^{2(x-3)} = 2^{5x}\\\\2(x-3) = 5x\\\\2x - 6 - 5x = 0\\\\-3x = 6\\\\\boxed{\textbf{x = -2}}$

ответ: -2.

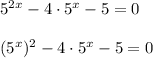
$5^{2x} - 4\cdot 5^x - 5 = 0\\\\(5^x)^2 - 4\cdot 5^x - 5 = 0$

Введём замену: 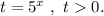$t = 5^x\ ,\ t 0.$

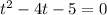
t^2 - 4t - 5 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -5\\t_{1}+t_{2} = 4\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 5; t = -1}$

Но так как 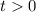t 0 , то -1 не является решением этого уравнения. Выполняем обратную замену:

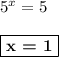
$5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

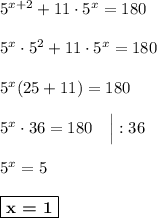
$5^{x+2} + 11\cdot 5^x = 180\\\\5^x \cdot 5^2 + 11\cdot 5^x = 180\\\\5^x(25+11) = 180\\\\5^x\cdot 36 = 180\ \ \ \Big| :36\\\\5^x = 5\\\\\boxed{\textbf{x = 1}}$

ответ: 1.

$9^{\sqrt{x-5}} - 27 = 6\cdot 3^{\sqrt{x-5}}$

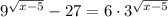
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:

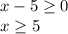
$x - 5 \geq 0\\x \geq 5$

Продолжаем решение:

$(3^2)^{\sqrt{x-5}} - 6\cdot 3^{\sqrt{x-5}} - 27 = 0\\\\(3^{\sqrt{x-5}})^2 - 6\cdot 3^{\sqrt{x-5}} - 27 = 0$

Введём замену: 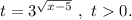$t = 3^{\sqrt{x-5}}\ ,\ t0.$

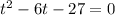
t^2 - 6t - 27 = 0

По теореме Виета:

$\begin{equation*}\begin{cases}t_{1}t_{2} = -27\\t_{1}+t_{2} = 6\end{cases}\end{equation*}\ \ \ \ \ \Big|\ \boxed{t = 9; t = -3}$

Но так как 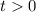t 0 , то -3 не является решением этого уравнения. Выполняем обратную замену:

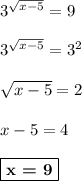
$3^{\sqrt{x-5}} = 9\\\\3^{\sqrt{x-5}} = 3^2\\\\\sqrt{x-5} = 2\\\\x - 5 = 4\\\\\boxed{\textbf{x = 9}}$

ответ: 9.

4,5(82 оценок)

Ответ:

хорошист547

21.08.2021

x2 + 4x + 8 = 0

Найдем дискриминант квадратного уравнения:

D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16

Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.

4x2 - 12x + 9 = 0

Найдем дискриминант квадратного уравнения:

D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0

Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:

x = 122·4 = 1.5

3x2 - 4x - 1 = 0

Найдем дискриминант квадратного уравнения:

D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28

Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:

x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024

x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635

2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.

4,8(37 оценок)

Это интересно:

Образование-и-коммуникации

21.09.2020

Как убедить человека рассказать свой секрет? Открываем профессиональные секреты психологии...

Здоровье

10.07.2021

Голубые глаза: миф или реальность?...

Компьютеры-и-электроника

04.07.2022

Как удалить историю поиска в iPod Touch: шаги по настройке конфиденциальности...

Стиль-и-уход-за-собой