ответ: Первый кран наполнит пустую ванну за 18 минут; второй кран опорожнит полную ванну за 12 минут.
Пошаговое объяснение: Пусть вся ванна 1 (единица), а х минут это время за которое первый кран наполнит ванну, тогда время за которое второй кран опорожнит ванну, будет х-6 минут. Производительность первого крана на наполнение будет 1/х; производительность второго крана на опорожнение будет 1/(х-6) , а совместная производительность на опорожнение ванны 1/36. Составим уравнение:
1/(х-6) - 1/х = 1/36
36х-36(х-6)=х(х-6)
х²-6х-216=0
D=900
х₁=-12 (мин) не подходит, т.к. время не может быть отрицательным.
х₂=18 (мин) время за которое первый кран наполнит пустую ванну.
18-6=12 (мин) время за которое второй кран опорожнит полную ванну.
Объяснение:
5) Пусть первая бригада изготовила X деталей, тогда вторая бригада изготовила (X+5) деталей, а третья (х+5)-15 деталей. Составим уравнение:
х+х+5+х+5-15=100
x+x+x=100+15-5-5
3x=105 |:3
x=35 (деталей) - изготовила первая бригада
35+5=40 (деталей) изготовила вторая бригада
40-15=25 (деталей) - изготовила третья бригада
ответ: Первая - 35 деталей, Вторая - 40 деталей, Третья - 25 деталей
6) Пусть один альбом стоит х рублей, один карандаш стоит y рублей, составим систему уравнений:
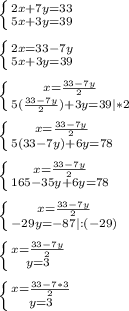
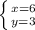
ответ: 1 альбом стоит 6 рублей, 1 карандаш стоит 3 рубля
7) на фото

Решение:
1. Воспользуемся формулами разность синусов и сумма косинусов:
Заметим, что оба равенства содержат один и тот же член:
В получившихся равенствах левые части равны, значит, равны и правые части:
Преобразуем данное равенство:
Теперь используем формулы понижения степени синуса и косинуса:
Преобразуем данное равенство:
n²(1-cos(x-y))=m²(1+cos(x-y));
n²-n²cos(x-y)=m²+m²cos(x-y);
m²cos(x-y)+n²cos(x-y)=n²-m²;
cos(x-y)(m²+n²)=n²-m²;
Используя основное тригонометрическое тождество, выразим sin(x-y):
ответ: