1. Область определения - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет
2. Пересечение с осью Х. Y=0
При х1 = x2 = - 2, x3 = 1
3. Пересечение с осью У. У(0) = -4
4. Поведение на бесконечности.
limY(-∞) = - ∞ и limY(+∞) = +∞
Горизонтальной асимптоты - нет
5. Исследование на чётность.
Y(-x) ≠ - Y(x)
Функция ни чётная ни нечетная - общего вида..
6. Производная функции.
Y'(x)= 3*x² + 6*x = 3*x*(x+2) = 0
7. Корень при Х= - 2.
Возрастает - Х∈(-∞;-2)∪(0;+∞)
максимум - Y(-2) =0
минимум - Y(0) = - 4
Убывает - X∈(-2;0)
8. Вторая производная
Y"(x) = 6*x +6 = 6*(x+1)
9. Точка перегиба
Y"(x)=0 при X=-1
Выпуклая - Х∈(-∞;-1] Вогнутая - Х∈[-1;+∞).
10. График в приложении.
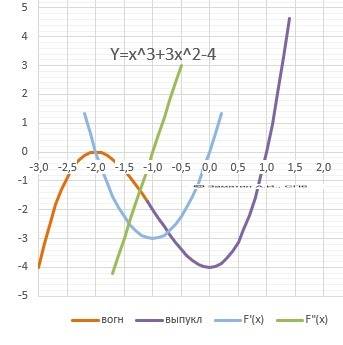
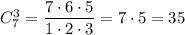
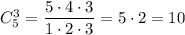
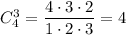
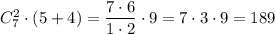
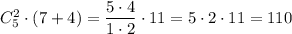
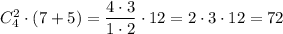
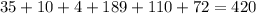
Пусть x-y =r, тогда
2r-11r+5=0
-9r+5=0
-9r=-5
r=5/9
R=x-y
x-y=5/9
2x+3y=25, возьмём коэффициенты и на их сумму разделим 25
x+Y=5
Подбираем таких два числа, чтобы их разность была равна 5/9, а сумма =5
Для этого решаем систему уравнений:
x-y=5/9
x+Y=5
(Представлен решения системы уравнений сложением)
2x= 5 5/9
2x= 50/9
x = 50/9*2=50/18
x=2 7/9
Подсталяем корень в уравнение, чтобы найти следующую переменную
2 7/9 - Y =5/9
-Y= -2 7/9 + 5/9
y = 2 7/9 - 5/9
Y = 2 2/9
ответ: 2 7/9; 2 2/9