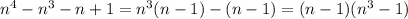
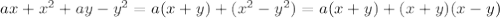
Сумма n нечетных последовательных чисел это арифмитеческая прогрессия с первым членом 1 и разностью 2
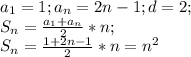
так как n^2 делится на n, то тем самым мы доказали,что сумма n нечётных последовательных чисел делится на n. Доказано
ОТКУДА МНЕ МОЖЕТ БЫТЬ ИЗВЕСТНО В КАКОМ КЛАССЕ УЧИШЬСЯ, ЕСЛИ ХАРАКТЕР ЗАДАЧИ ОЛИМПИАДНЫЙ?
вариант 2 (вывод формулы "вручную")
S=1+3+5+7+..+(2n-1)
S=(2n-1)+(2n-3)+...+7+5+3+1;
2S=1+3+5+7+..+(2n-1)+(2n-1)+(2n-3)+...+7+5+3+1=(1+(2n-1))+(3+(2n-3))+...=n скобок в каждой сумма равна числу 2n=n*2n=2n^2 (два єн в квадрате)
S=n^2
так как n^2 делится на n, то тем самым мы доказали,что сумма n нечётных последовательных чисел делится на n. Доказано
вариант 3 (с использованием метода математической индукции)
Гипотеза. Ищем формулу
2*1-1=1=1=1^2
2*1-1+2*2-1=1+3=4=2^2
2*1-1+2*2-1+2*2-1=1+3+5=9=3^2
напрашивается формула 1+3+5+...+(2n-1)=n^2
Докажем методом математической индукции, что єто ИСТИННО.
База индукции n=1: 1=1^2 верно
Гипотеза индукции. Пусть при n=k: 1+3+5+...+(2k-1)=k^2
Индукционный переход. Докажем, что тогда утверждение истинно и при n=k+1
1+3+5+...+(2k-1)+(2k+1)=используем гипотезу=k^2+(2k+1)=используем формулу квадрата двучлена=(k+1)^2, что и требовалось доказать
По принципу математической индукции 1+3+5+...+(2n-1)=n^2.
так как n^2 делится на n, то тем самым мы доказали,что сумма n нечётных последовательных чисел делится на n. Доказано
вариант4 (геометрический)
возьмем квадрат размерами 1*1 его площадь 1
возьмем достроем его 3 квадратами 1*1(их площадь 3*1*1=3), получится большой квадрат 2*2
(1+3=2*2)
возьмем достроим новый квадрат 5 квадратами 1*1(их площадь 5*1*1=5), получится большой квадрат 3*3
(1+3+5=)
и т.д.сумма площадей "маленьких n квадратов" равна площади большого квадрата n*n
1+3+5+...+(2n-1)=n^2
видим ,что так как n^2 делится на n, то тем самым мы доказали,что сумма n нечётных последовательных чисел делится на n. Доказано
вариант 5, разобьем сумму на подсуммы первый с последним, второй с предоследним, и т.д., если количевство нечетных чисел нечетно среднее слагаемое само по себе
1+2n-1=2n делится на n
3+2n-3=2n делится на n
...
n/2-1+n/2+1=n делится на n
и ("особое слагаемое")
n делится делится на n
Каждое из слагаемых делится на n, значит и вся сумма делится на n