ответ: 20 часов.
Объяснение: Пусть весь бассейн 1 (единица), тогда совместная производительность двух насосов будет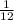 
(бас/ч). Возьмем, что за х часов первый насос может наполнить весь бассейн самостоятельно, тогда его производительность будет 
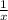(бас/ч). Т.к. второй насос наполняет половину бассейна на 5 часов дольше, то целый бассейн он наполнит на 5÷(1/2)=10 часов дольше первого и соответственно производительность второго насоса будет 
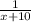(бас/ч). Составим уравнение:
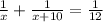
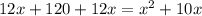
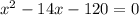
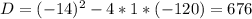
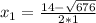
x₁=(-6) (ч) Не подходит, т.к. время не может быть отрицательное.
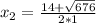
х₂=20 (ч) нужно первому насосу, чтобы наполнить бассейн водой, работая самостоятельно.
