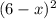/![\sqrt[2]{6-x}](/tpl/images/0518/6758/4344a.png)
= ![\sqrt[3]{ (6-x)^2}](/tpl/images/0518/6758/63180.png)
Если верна пропорция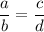 
, то по основному свойству пропорции произведение крайних членов равно произведению средних членов:
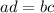
Рассмотрим пропорцию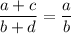 
. Проверим, равно ли произведение крайних и произведение средних членов:
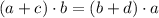
Слагаемое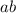 
взаимно уничтожается.
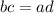
Это равенство верно, так как оно получено из исходной верной пропорции.
Рассмотрим пропорцию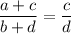 
. Проверим, равно ли произведение крайних и произведение средних членов:
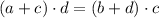
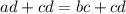
Слагаемое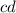 
взаимно уничтожается.
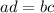
Это равенство также верно, так как оно получено из исходной верной пропорции.
Объяснение:
Можно доказать более наглядно. Вариант с отрицательностью дискриминанта, по-хорошему, требует обоснование этого вывода.
Предлагаю следующий вариант:
х² - 6х + 13 = 0
Преобразуем. Выразим 13 как 9+4
х² - 6х + 9 + 4 = 0
х² - 2•3х + 3² + 4 = 0
(х - 3)² + 4 = 0
или даже:
(х - 3)² + 2² = 0
Мы получили в левой части сумму квадрата некоего числа и 4. Как известно, квадрат любого числа не может быть меньше нуля. А следовательно выражение в левой части не может быть меньше
0 + 4 = 4
Значит, левая часть уравнения всегда >= 4,
и ни при каких значениях х не может быть равна правой части (нулю).
Следовательно, уравнение корней не имеет
