Алгебра: 4х-2у=3 13х+6у= -1 решите систему уравнений

4х-2у=3 13х+6у= -1 решите систему уравнений

👇

Увидеть ответ

Ответ:

tiamaressp035gw

02.02.2021

файл

4,6(49 оценок)

Ответ:

vixoreva98

02.02.2021

домножим первое уравнение на 3, имеем 12х-6у=9

13+6у=-1

Сложим эти два уравнения. получим 25х=8, откуда х=8/25

Подставим в первое уравнение, 4 *(8/25)-2у=3

-2у=3-(32/25)=43/25

y=-43/50

4,6(58 оценок)

Открыть все ответы

Ответ:

rekiol544

02.02.2021

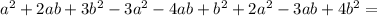
a^2+2ab+3b^2-3a^2-4ab+b^2+2a^2-3ab+4b^2=

Приведем подобные члены. Я их сгруппирую для наглядности:
=a^2+2a^2-3a^2+b^2+3b^2+4b^2+2ab-4ab-3ab=

Различия между ними - это степень и сама буква неизвестного значения: "a" и "b".
Далее просто складываем и вычитаем в зависимости от знака подобные члены. Все упрощение, условно, сводится в 3 действия, так как 3 вида значений:
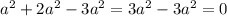
1) a^2+2a^2-3a^2=3a^2-3a^2=0

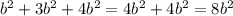
- Тут вынес знак минуса за скобку, чтобы было понятно, что разность -4ab-3ab дает сумму с отрицательным знаком.
В итоге записываем полученное выражение:
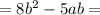
=8b^2-5ab=

На этом можно остановиться, можно вынести одинаковые значения за общую скобку. Этим значением является буква b, тогда запись выражения примет вид:
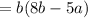
=b(8b-5a)

Но нужно помнить, что когда мы выносим одинаковые члены за скобку, то от чего мы их отделяем - делим на то самое отделяемое значение. Если расписать действие переноса буквы b за скобку по шагам, то будет более понятно:
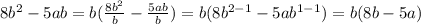
$8b^2-5ab=b( \frac{8b^2}{b}- \frac{5ab}{b})=b(8b^{2-1}-5ab^{1-1})=b(8b-5a)$

Решение без пояснений:
a^2+2ab+3b^2-3a^2-4ab+b^2+2a^2-3ab+4b^2=a^2+2a^2-3a^2+b^2+3b^2+4b^2+2ab-4ab-3ab=8b^2-5ab=b(8b-5a)

a^2+2ab+3b^2-3a^2-4ab+b^2+2a^2-3ab+4b^2=a^2+2a^2-3a^2+b^2+3b^2+4b^2+2ab-4ab-3ab=8b^2-5ab=b(8b-5a)

---------------------------------------------------------------------
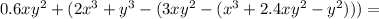
2. 0.6xy^2+(2x^3+y^3-(3xy^2-(x^3+2.4xy^2-y^2)))=

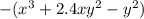Тут самое главное правильно раскрыть скобки с учетом знаков перед ними, а далее все как в первом решении. Начинать раскрытие скобок нужно изнутри, то есть от выражения " -(x^3+2.4xy^2-y^2)

"
Распишу раскрытие скобок по действиям:
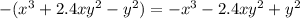
1) -(x^3+2.4xy^2-y^2)=-x^3-2.4xy^2+y^2

-(3xy^2-x^3-2.4xy^2+y^2)=-3xy^2+x^3+2.4xy^2-y^2

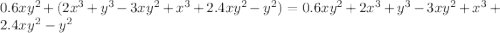
0.6xy^2+(2x^3+y^3-3xy^2+x^3+2.4xy^2-y^2)=0.6xy^2+2x^3+y^3-3xy^2+x^3+2.4xy^2-y^2

В итоге получили выражение под пунктом 3.
Далее, приводя подобные члены получим:
=3x^3+y^3-y^2

Далее можем также вынести за скобку одинаковые члены, но в этом нет смысла, так как не принесет упрощения.

Решение без пояснений:
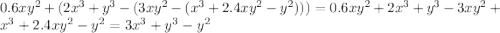
0.6xy^2+(2x^3+y^3-(3xy^2-(x^3+2.4xy^2-y^2)))=0.6xy^2+2x^3+y^3-3xy^2+x^3+2.4xy^2-y^2=3x^3+y^3-y^2

0.6xy^2+(2x^3+y^3-(3xy^2-(x^3+2.4xy^2-y^2)))=0.6xy^2+2x^3+y^3-3xy^2+x^3+2.4xy^2-y^2=3x^3+y^3-y^2

4,6(77 оценок)

Ответ:

mulz

02.02.2021

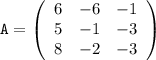
$\displaystyle\tt A=\left(\begin{array}{ccc}6&-6&-1\\5&-1&-3\\8&-2&-3\end{array}\right)$

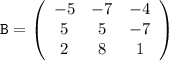
$\displaystyle\tt B=\left(\begin{array}{ccc}-5&-7&-4\\5&5&-7\\2&8&1\end{array}\right)$

---------------------------------

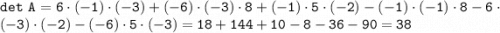
$\displaystyle\tt det\ A=6\cdot(-1)\cdot(-3) + (-6)\cdot(-3)\cdot8 + (-1)\cdot5\cdot(-2) - (-1)\cdot(-1)\cdot8 - 6\cdot(-3)\cdot(-2) - (-6)\cdot5\cdot(-3) = 18 + 144 + 10 - 8 - 36 -90=38$

---------------------------------

$\displaystyle\tt A\cdot B=\left(\begin{array}{ccc}6&-6&-1\\5&-1&-3\\8&-2&-3\end{array}\right)\cdot\left(\begin{array}{ccc}-5&-7&-4\\5&5&-7\\2&8&1\end{array}\right)=\left(\begin{array}{ccc}-62&-80&17\\-36&-64&-16\\-56&-90&-21\end{array}\right)$

c₁₁ = a₁₁ · b₁₁ + a₁₂ · b₂₁ + a₁₃ · b₃₁ = 6 · (-5) + (-6) · 5 + (-1) · 2 = (-30) - 30 - 2 = -62

c₁₂ = a₁₁ · b₁₂ + a₁₂ · b₂₂ + a₁₃ · b₃₂ = 6 · (-7) + (-6) · 5 + (-1) · 8 = (-42) - 30 - 8 = -80

c₁₃ = a₁₁ · b₁₃ + a₁₂ · b₂₃ + a₁₃ · b₃₃ = 6 · (-4) + (-6) · (-7) + (-1) · 1 = (-24) + 42 - 1 = 17

c₂₁ = a₂₁ · b₁₁ + a₂₂ · b₂₁ + a₂₃ · b₃₁ = 5 · (-5) + (-1) · 5 + (-3) · 2 = (-25) - 5 - 6 = -36

c₂₂ = a₂₁ · b₁₂ + a₂₂ · b₂₂ + a₂₃ · b₃₂ = 5 · (-7) + (-1) · 5 + (-3) · 8 = (-35) - 5 - 24 = -64

c₂₃ = a₂₁ · b₁₃ + a₂₂ · b₂₃ + a₂₃ · b₃₃ = 5 · (-4) + (-1) · (-7) + (-3) · 1 = (-20) + 7 - 3 = -16

c₃₁ = a₃₁ · b₁₁ + a₃₂ · b₂₁ + a₃₃ · b₃₁ = 8 · (-5) + (-2) · 5 + (-3) · 2 = (-40) - 10 - 6 = -56

c₃₂ = a₃₁ · b₁₂ + a₃₂ · b₂₂ + a₃₃ · b₃₂ = 8 · (-7) + (-2) · 5 + (-3) · 8 = (-56) - 10 - 24 = -90

c₃₃ = a₃₁ · b₁₃ + a₃₂ · b₂₃ + a₃₃ · b₃₃ = 8 · (-4) + (-2) · (-7) + (-3) · 1 = (-32) + 14 - 3 = -21

---------------------------------

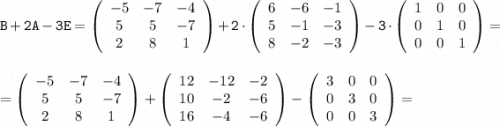
$\displaystyle\tt B+2A-3E=\left(\begin{array}{ccc}-5&-7&-4\\5&5&-7\\2&8&1\end{array}\right)+2\cdot\left(\begin{array}{ccc}6&-6&-1\\5&-1&-3\\8&-2&-3\end{array}\right)-3\cdot\left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)=\\\\\\\displaystyle\tt=\left(\begin{array}{ccc}-5&-7&-4\\5&5&-7\\2&8&1\end{array}\right)+\left(\begin{array}{ccc}12&-12&-2\\10&-2&-6\\16&-4&-6\end{array}\right)-\left(\begin{array}{ccc}3&0&0\\0&3&0\\0&0&3\end{array}\right)=$

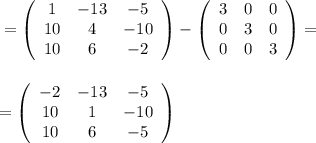
$\displaystyle\tt=\left(\begin{array}{ccc}1&-13&-5\\10&4&-10\\10&6&-2\end{array}\right)-\left(\begin{array}{ccc}3&0&0\\0&3&0\\0&0&3\end{array}\right)=\\\\\\\displaystyle\tt=\left(\begin{array}{ccc}-2&-13&-5\\10&1&-10\\10&6&-5\end{array}\right)$

----------------------------------------

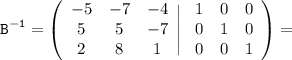
$\displaystyle\tt B^{-1}=\left(\begin{array}{ccc}-5&-7&-4\\5&5&-7\\2&8&1\end{array}\Bigg|\left\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\right)=$

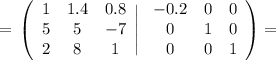
$=\displaystyle\tt \left(\begin{array}{ccc}1&1.4&0.8\\5&5&-7\\2&8&1\end{array}\Bigg|\left\begin{array}{ccc}-0.2&0&0\\0&1&0\\0&0&1\end{array}\right)=$

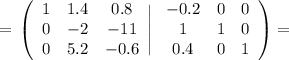
$=\displaystyle\tt \left(\begin{array}{ccc}1&1.4&0.8\\0&-2&-11\\0&5.2&-0.6\end{array}\Bigg|\left\begin{array}{ccc}-0.2&0&0\\1&1&0\\0.4&0&1\end{array}\right)=$

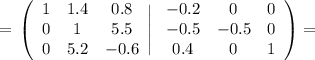
$=\displaystyle\tt \left(\begin{array}{ccc}1&1.4&0.8\\0&1&5.5\\0&5.2&-0.6\end{array}\Bigg|\left\begin{array}{ccc}-0.2&0&0\\-0.5&-0.5&0\\0.4&0&1\end{array}\right)=$

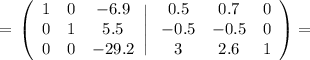
$=\displaystyle\tt \left(\begin{array}{ccc}1&0&-6.9\\0&1&5.5\\0&0&-29.2\end{array}\Bigg|\left\begin{array}{ccc}0.5&0.7&0\\-0.5&-0.5&0\\3&2.6&1\end{array}\right)=$

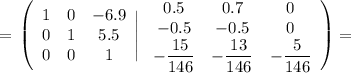
$=\displaystyle\tt \left(\begin{array}{ccc}1&0&-6.9\\0&1&5.5\\0&0&1\end{array}\Bigg|\left\begin{array}{ccc}0.5&0.7&0\\-0.5&-0.5&0\\-\dfrac{15}{146}&-\dfrac{13}{146}&-\dfrac{5}{146}\end{array}\right)=$

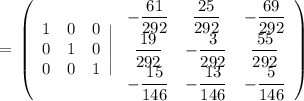
$=\displaystyle\tt \left(\begin{array}{ccc}1&0&0\\0&1&0\\0&0&1\end{array}\Bigg|\left\begin{array}{ccc}-\dfrac{61}{292}&\dfrac{25}{292}&-\dfrac{69}{292}\\\dfrac{19}{292}&-\dfrac{3}{292}&\dfrac{55}{292}\\-\dfrac{15}{146}&-\dfrac{13}{146}&-\dfrac{5}{146}\end{array}\right)$

$\displaystyle\tt B^{-1}=\left(\begin{array}{ccc}-\dfrac{61}{292}&\dfrac{25}{292}&-\dfrac{69}{292}\\\dfrac{19}{292}&-\dfrac{3}{292}&\dfrac{55}{292}\\-\dfrac{15}{146}&-\dfrac{13}{146}&-\dfrac{5}{146}\end{array}\right)$