№6
3х – 5 (2х + 1) = 3 ( 3 – 2х)
3х–10х–5=9–6х
3х–10х+6х=9+5
–х=14
х=–14
ответ: –14
№5
х²–3х–3у–у²= –3(х+у)+х²–у²= –3(х+у)+(х+у)(х–у)= (х+у)(–3+х–у)
№1
(а +6)²–2а(3 – 2а)=а²+12а+36–6а+4а²= 5а²+6а+36
№2
Система:
5х – 2у = 11
4х – у = 4 |*(–2)
Система:
5х – 2у = 11 (Ур 1)
–8х+2у=–8 (Ур 2)
Сложим уравнения 1 и 2, получим:
–3х=3
х=–1
Подставим значение х у уравнение 1, получим:
5*(–1)–2у=11
–5–2у=11
–2у=16
у=–8
ответ: х=–1; у=–8
№4
Пусть х км– путь в третий день, тогда во второй х+5, а в первый (х+5)+10
Составим уравнение:
х+(х+5)+(х+5+10)=50
х+х+5+х+5+10=50
3х=50–10–5–5
3х=30
х=10
Тогда в третий день 10 км, во второй 10+5=15 км, в первый 10+5+10=25 км
ответ: Первый день 25 км; второй день 15 км; третий день 10 км.
№3
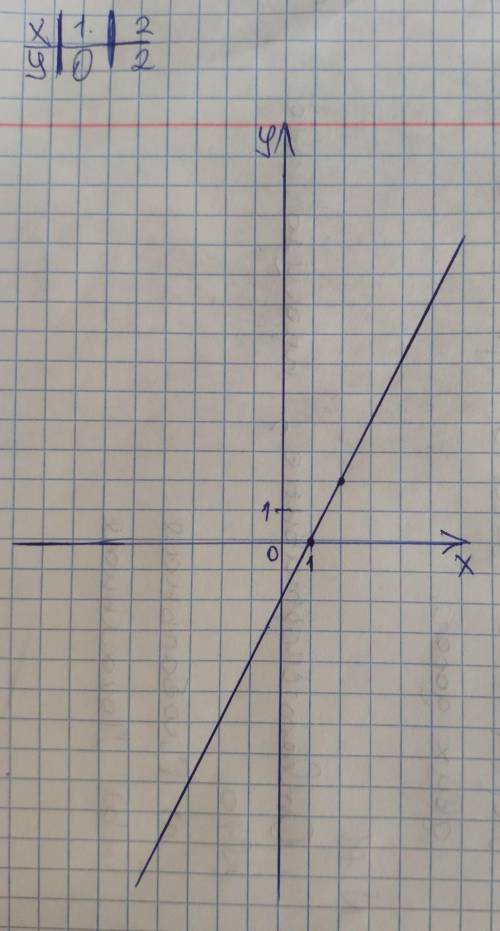
Кординаты точки А х=–10; у=–20.
Подставим значения в функцию у = 2х – 2, получим:
–20=2*(–10)–2
–20=–20–2
–20≠–22
Следовательно график НЕ проходит через точку А.
График во вложении
ответ: 2/3
Объяснение:
Решим неравенства :
x^2-9 <= 0
(x-3)(x+3) <=0
x∈ [-3 ; 3]
|x+3| >=2
x+3>=2
x+3<=-2
x∈ [-∞ ;-5] ∪ [-1;+∞]
Найдем пересечение решений неравенств :
x∈ [ -1 ;3 ]
Все исходы показывает длина отрезка : [-3 ; 3] (все решения неравенства x^2-9 <= 0 )
Lобщ = |-3| +|3| = 6 ед ( cчитаем за 1 единицу длину отрезка от числа 0 до числа 1 на координатной прямой)
Благоприятные исходы показывает длина отрезка x∈ [ -1 ;3 ] ( те решения неравенства x^2-9 <= 0 , что являются решениями неравенства |x+3| >=2 )
Lблаг = |-1| +|3| = 4
Тогда вероятность :
P = Lблаг/Lобщ = 4/6 = 2/3
**************
так как основание меньше 1 то неравенство меняет знак
******************
ОДЗ X>3.x≠4
1) 3<x<4 основание меньше еденицы
решений нет
2) x>4
решение (4;8]