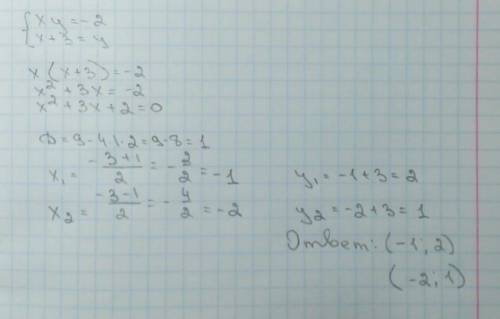
1. Найти производную функции: f(x).
2. Найти точки, в которых производная равна нулю: f(x)=0 x1, x2,...
3. Определить принадлежность точек х1, х2, … отрезку [a; b]: пусть x1a;b , а x2a;b .
4. Найти значения функции в выбранных точках и на концах отрезка: f(x1), f(x2),..., f(xa), f(xb),
5. Выбор наибольшего и наименьшего значений функции из найденных.
Замечание. Если на отрезке [a; b] имеются точки разрыва, то необходимо в них вычислить односторонние пределы, а затем их значения учесть в выборе наибольшего и наименьшего значений функции.
первое легко решается письменно
из второго ур-я системы выразим у: у=5+х, подставим в первое: 5+х=|х^2+6x+5|
исходя из определения модуля запишем: 1) х^2+6x+5, если х^2+6x+5>0
|х^2+6x+5|= 2)-(х^2+6x+5), если х^2+6x+5<0
Рассмотрим первое: 5+х=х^2+6x+5 , х^2+5x=0, х1=0, х2=-5, решим неравенство и проверим, удовлетворяет ли ли данные корни условию: х^2+6x+5>0 х<-6, x>-1
х2=-5 не удовлетворяет условию. Тогда получили первую пару корней:(0;5)
Рассмотрим втрое аналогично: 5+х=-(х^2+6x+5), х^2+7х+10=0, х2=-2, х3=-5
решим неравенство х^2+6x+5<0, х принадлежит(-6;-1) оба корня удовл. условию
получили еще две пары: (-2;3) и (-5;0)
если нужно граф. решение, то там получится три пересечения
что бы посторить график под модулем нужно построить две параболы и выкинуть не удовлетвор области определения:1) х^2+6x+5, при х^2+6x+5>0, в данном случае выкидываешь все что, принадлежит промежутку (-6;-1)
-(х^2+6x+5), при х^2+6x+5<0, эта парабола обратная предыдущей, в данном случае выкидываем при х<-6 и x>-1
останется красивый график .Осталось только постоить
есть еще более простоий переноса) но я предпочитаю это, ибо меньше шансов ошибиться
Сейчас остальные порешаю)