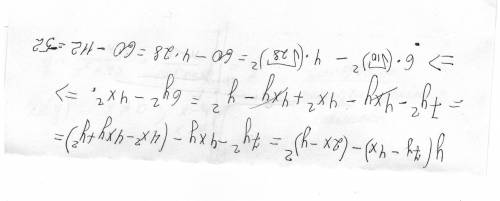
Пусть х км/ч - собственная скорость катера, тогда (х + 2) км/ч - скорость катера по течению реки, (х - 2) км/ч - скорость катера против течения реки. Уравнение:
24/(х+2) + 24/(х-2) = 3,5
24 · (х - 2) + 24 · (х + 2) = 3,5 · (х -2) · (х + 2)
24х - 48 + 24х + 48 = 3,5 · (х² - 2²)
48х = 3,5х² - 14
3,5х² - 48х - 14 = 0
D = b² - 4ac = (-48)² - 4 · 3,5 · (-14) = 2304 + 196 = 2500
√D = √2500 = 50
х₁ = (48-50)/(2·3,5) = (-2)/7 - не подходит, так как < 0
х₂ = (48+50)/(2·3,5) = 98/7 = 14
ответ: 14 км/ч.
Проверка:
24 : (14 - 2) + 24 : (14 + 2) = 3,5
24 : 12 + 24 : 16 = 3,5
2 + 1,5 = 3,5 (ч) - время, затраченное на путь туда и обратно
y=Π/3-x
sin x+cos(Π/3-x)=1
sin x+cos Π/3*cos x+sin Π/3*sin x=1
sin x*(1+√3/2)+cos x*1/2=1
Переходим к половинным аргументам и умножаем все на 2.
2sin(x/2)*cos(x/2)*(2+√3) + cos^2(x/2) - sin^2(x/2) = 2cos^2(x/2)+2sin^2(x/2)
Переносимости все в одну сторону
3sin^2(x/2) - (4+2√3)*sin(x/2)*cos(x/2) + cos^2(x/2) = 0
Делим все на cos^2(x/2)
3tg^2(x/2)-(4+2√3)*tg(x/2)+1=0
Замена t=tg(x/2)
3t^2-(4+2√3)*t+1=0
Получили обычное квадратное уравнение
D/4=(2+√3)^2-3*1=4+4√3+3-3= 4+4√3
t1=tg(x/2)=[2+√3-√(4+4√3)]/3
t2=tg(x/2)=[2+√3+√(4+4√3)]/3
Соответственно
x1=2*arctg(t1)+Π*n; y1=Π/3-x1
x2=2*arctg(t2)+Π*n; y2=Π/3-x2