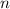 месяцев взяли
месяцев взяли 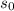 рублей. Тогда:
рублей. Тогда: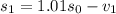
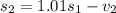
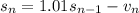 ,
,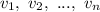 - выплаты в 1, 2, ..., n месяце. Заметим, что последний остаток
- выплаты в 1, 2, ..., n месяце. Заметим, что последний остаток 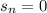 , так как через n месяцев весь кредит выплачен.
, так как через n месяцев весь кредит выплачен.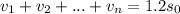
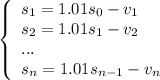 сложим все уравнения, после чего слагаемые вида
сложим все уравнения, после чего слагаемые вида 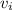 перенесем влево, а слагаемые вида
перенесем влево, а слагаемые вида 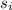 - вправо.
- вправо.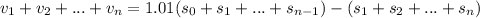
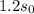 :
: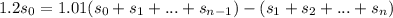
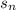 :
: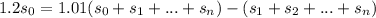
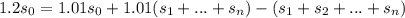
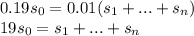
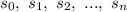 уменьшаются равномерно, то есть составляют арифметическую прогрессию.
уменьшаются равномерно, то есть составляют арифметическую прогрессию. :
: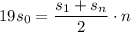
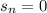 , то выражение упрощается:
, то выражение упрощается: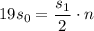
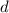 . Тогда:
. Тогда: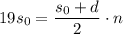
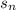 через первый член и разность прогрессии:
через первый член и разность прогрессии: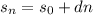
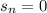 , то
, то 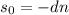 . Подставляем в соотношение:
. Подставляем в соотношение: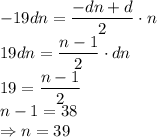
x²(6+x)≠0
x≠0,x≠-6
x∈(-∞;-6) U (-6;0) U (0;∞)
2)У =19х-12/(5х-4)(х-13)
(5x-4)(x-13)≠0
x≠0,8;x≠13
x∈(-∞;0,8) U (0,8;13) U (13;∞)
3)У = 2х²-5х+2/3х²-х+10
3x²-x+10≠0
D=1-120=-119<0
при любом х выражение больше 0
x∈R
4)У = √2-х
2-x≥0
x≤2
x∈(-∞;2]
5)У = √2х^6+х²
Любое число в четной степени больше или равняется 0.Сумма положительных всегда положительна.
x∈R
6)У = √20-х²
20-x²≥0
(2√5-x)(2√5+x)≥0
x∈[-2√5;2√5]
7)У = √5- 1/5 Х²
5-1/5x²≥0
(25-x²)/5≥0
(5-x)(5+x)≥0
x∈[-5;5]
8)У = х²/√х²-8х+15
x²-8x+15>0
x1+x2=8 U x18x2=15
x1=3 U x2=5
x∈(-∞;3) U (5;∞)