Объяснение:
Разложим на множители выражение в числителе и знаменателе.
\begin{gathered}y=\frac{24-12x}{2x-x^2}\\y=\frac{-12(x-2)}{-x(x-2)}\\\left \{ {{y=\frac{12}{x} } \atop {x\neq 2}} \right.\end{gathered}
y=
2x−x
2
24−12x
y=
−x(x−2)
−12(x−2)
{
x
=2
y=
x
12
Это гипербола, которая лежит в 1 и 3 четверти и имеет асимптоты, которыми являются оси координат.
Отметим 2 точки, которые принадлежат этой функции на координатной плоскости для более точно построения.
x=12 --> y=1; (12;1)
x=1 --> y=12; (1;12)
И проведём через них нашу гиперболу.
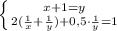
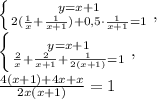
2x² - 10x + 3x - 15 -(16 - x²)=2x + 5
2x² - 7x - 15 - 16 + x² = 2x + 5
3x² - 7x - 31 - 2x - 5 = 0
3x² - 9x - 36 = 0 сократить на 3
x² - 3x - 12 = 0
ответ D: x² - 3x - 12 = 0