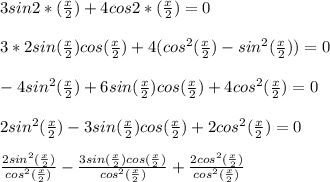 =0
=0
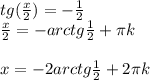 ,
,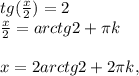
 k∈Z;
k∈Z;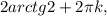 k∈Z.
k∈Z.
ответ
Соотношение параметров квадрата
Приведём формулы периметра Р и площади S квадрата через длину стороны а.
периметр квадрата Р равен учетверённому размеру его стороны а: Р = 4 * а;
площадь квадрата S равна квадрату его стороны а: S = a²;
периметр и площадь квадрата связаны между собой. так как в их формулах общий параметр - сторона квадрата: S = P² / 16.
Для понятного объяснения задачи увеличим по заданию его сторону в 3 раза.Тогда новая сторона квадрата станет а1 = 3 * а.
Вычисление увеличения периметра и площади квадрата
Чтобы узнать, как при этом изменились периметр и площадь квадрата, подставим в формулы Р и S вместо "а" новое значение стороны "а1". Тогда:
Р1 = 4 * а1 = 4 * (3 * а ) = 12 * а;
S1 = а1² = (3 * а)² = 9 * а².
После того, как выразили новый периметр Р1 и площадь S1 через начальное значение стороны "а", можно ответить на вопрос задания:
для вычислений используем написанные выше формулы для площади S и периметра P;
чтобы узнать, во сколько раз увеличится периметр квадр
чтобы узнать, во сколько раз увеличится площадь квадрата, нужно разделить S1 на S.
Согласно выше сказанного, ответим на вопросы задания:
во сколько раз увеличился периметр квадрата, для чего разделим (Р1 : Р) = (12 * а) : (4 * а) = 3 (раза);
во сколько раз увеличится площадь квадрата, для чего разделим (S1 : S) = (9 * а²) : (а²) = 9 (раз).
заметим, что если периметр квадрата увеличился в 3 раза, как и сторона квадрата, то площадь, увеличивается в (3)² = 9 раз.
ответ: периметр увеличится в 3 раза, площадь увеличится в 9 раз.
Объяснение:
здесь показан ответ только цифрами 9 и 3 А ты вставь цифры которые даны в задание
неотрицательное число, квадрат которого равен a . Это число
обозначают √ a , число а называют подкоренным числом.
Если √ a = b , то b 2 = a , при а ≥ 0 и b ≥ 0 .
Например:
√ 0 = 0 ; √ 1 = 1 ; √ 4 = 2 ; √ 9 = 3 ; √ 0,09 = 0,3 ...
0 2 = 0 ; 1 2 = 1 ; 2 2 = 4 ; 3 2 = 9 ; 0,3 2 = 0,09 ...
Обратите внимание,
(−5) 2 = 25 , но √ 25 ≠ −5 , √ 25 = 5 .
Корень не может быть равен отрицательному числу.
√ −25 — нельзя вычислить.
Корень из отрицательного числа не существует.
Свойства квадратных корней
√ ab = √ a • √ b ;
√ ab = √ a√ b если а ≥ 0 и b > 0 ;
√ a 2n = a n если а ≥ 0 и n — натуральное число ;
(√ a) 2n = a n если а ≥ 0 и n — натуральное число .
Примеры вычисления выражений с корнями:
1) √ 50 • √ 32 = √ 25•2 • √ 16•2 =
= √ 25•√ 16•√ 2•√ 2 = 5•4•2 = 40 ;
2) √ 48√ 27 = √ 16•39•3 = √ 169 = √ 16√ 9 = 43 = 1 13 ;
3) √ 2 43 6 = √ 2 4√ 3 6 = √ (2 2) 2√ (3 3) 2 = 2 23 3 = 427 ;
4) √ 4 2125 = √ 4•25+2125 = √ 121√ 25 = 115 = 2 15 = 2,2 ;
5) √ 145 2−24 2 = √ (145−24)(145+24) = √ 121•169 =
= √ 121•√ 169 = 11•13 = 143 .