Question

Решите рациональные неравенства 11-(x+1)^2≥x (2x-8)^2-4x(2x-8)≥0 x(x+5)-2> 4x (1/3)x^2+3x+6< 0 x> (x^2/2)-4x+5(1/2)

Answer 1

$1)\; \; 11-(x+1)^2\geq x\\\\11-x^2-2x-1\geq x\\\\x^2+3x-10\leq 0\; ,\; \; x_1=-5\; ,\; x_2=2\; (teorema\; Vieta)\\\\znaki:\quad +++[-5\, ]---[\, 2\, ]+++\\\\x\in [-5,2\, ]\\\\2)\; \; (2x-8)^2-4x(2x-8)\geq 0\\\\4x^2-32x+64-8x^2+32x\geq 0\\\\-4x^2+64\geq 0\; |:(-4)\; \; \to \; \; x^2-16\leq 0\\\\(x-4)(x+4)\leq 0\; ,\qquad +++[-4\, ]---[\, 4\, ]+++\\\\x\in [-4,4\, ]\\\\3)\; \; x(x+5)-24x\\\\x^2+5x-4x-20\; \; \to \\\\x^2+x-20\; ,\; \; x_1=-2\; ,\; x_2=1\; (teorema\; Vieta)\\\\(x+2)(x-1)0\quad +++(-2)---(1)+++\\\\x\in (-\infty ,-2)\cup (1,+\infty )$

$4)\; \; \frac{1}{3}x^2+3x+6$

Answer 2

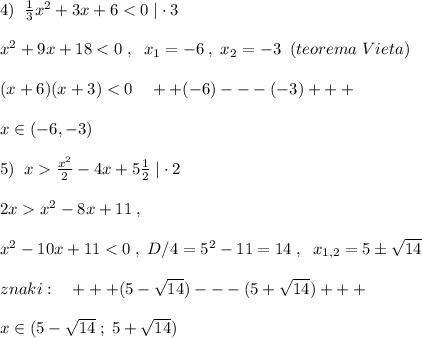
11-(x+1)²≥x

11-x²-2x-1≥x

x²+3x-10≤0

x²+3x-10=0 D=49 √D=7

x₁=2 x₂=-5

(x-2)(x+5)≤0

-∞+-5___-2++∞ ⇒

ответ: x∈[-5;2]

(2x-8)²-4x*(2x-8)≥0

(2x-8)(2x-8-4x)≥0

(2x-8)(-2x-8)≥0

-(2x-8)*(2x+8)≥0 |÷(-1)

4x²-64≤0 |÷4

x²-16≤0

(x-4)(x+4)≤0

-∞+-4-4++∞ ⇒

ответ: x∈[-4;4].

x*(x+5)-2>4x

x²+5x-2-4x>0

x²+x-2>0

x²+x-2=0 D=9 √D=3

x₁=1 x₂=-2 ⇒

(x-1)(x+2)>0

-∞+-2-1++∞ ⇒

ответ: x∈(-∞-2)U(1;+∞).

(1/3)*x²+3x+6<0 |×3

x²+9x+18<0

x²+9x+18=0 D=9 √D=3

x₁=-3 x₂=-6 ⇒

(x+3)(x+6)<0

-∞+-6--3++∞ ⇒

ответ: x∈(-6;-3).

x>(x²/2)-4x+5¹/₂

x>(x²/2)-4x+11/2 |×2

2x>x²-8x+11

x²-10x+11<0

x²-10x+11=0 D=56 √D=√56

x₁=5-√14 x₂=5+√14

-∞+5-√14-5+√14++∞ ⇒

ответ: x∈(5-√14;5+√14).