

 км/мин.
км/мин.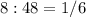 км/мин.
км/мин.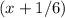 км/мин.
км/мин.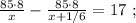
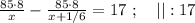
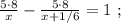
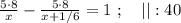
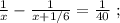
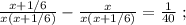
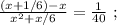
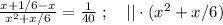
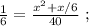
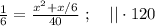
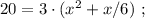
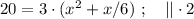
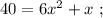
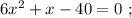
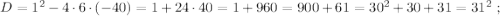
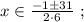
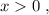 так, как это скорость,
так, как это скорость,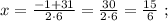
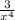 и
и 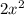 не поставлен никакой знак. Ну а поскольку арифметические знаки « * » и « : » в данном случае довольно бессмысленны, то скорее всего там « + » или « – ».
не поставлен никакой знак. Ну а поскольку арифметические знаки « * » и « : » в данном случае довольно бессмысленны, то скорее всего там « + » или « – ».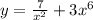 – исследовать функцию на чётность и найти её область определения.
– исследовать функцию на чётность и найти её область определения.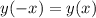 (I) ;
(I) ;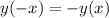 (II) ;
(II) ;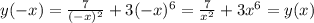 ;
;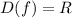 \ {0}
\ {0} 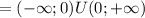
19-15х+30=26-8x -15x+8x=26-49 -7x=-21 x=3
6x+15=0 x=-2,5 2,4-0,8x=0 x=3
12x-5x+8=8+7x 12x-5x-7x=8-8 0×x=0 х любое число