Решить 2 задачи. до утра(!)
С подробным решением))
1. Первая труба пропускает на 6 литров воды в минуту меньше, чем 2я труба. Ск-ко литров воды в минуту пропускает 1я труба, если бак объемом 360 литров она заполняет на 10 минут медленнее, чем 2я труба?
Примем
S1 - скорость течения воды в 1-й трубе, литр/мин
S2 - скорость течения воды во 2-й трубе, литр/мин
S2=S1+6
360/S1=360/S2+10
360/S1-360/S2-10=0
(360*S2-360*S1-10*S1*S2)/(S1*S2)=0
(360*(S1+6)-360*S1-10*S1*(S1+6))=0
360*S1+2160-360*S1-10*S1^2-60*S1=0
-10*S1^2-60*S1+2160=0
S1^2+6*S1-216=0
Квадратное уравнение, решаем относительно S1:
Ищем дискриминант:
D=6^2-4*1*(-216)=36-4*(-216)=36-(-4*216)=36-(-864)=36+864=900;
Дискриминант больше 0, уравнение имеет 2 корня:
S1_1=(30-6)/2=24/2=12;
S1_2=(-30-6)/2=-36/2=-18.
Скорость теченя воды не может быть величиной отрицательной, поэтому ответ будет такой: 1-я труба пропускает 12 литр/мин
2. Т.Сойер и Г.Финн красят забор длиной в 100 метров. каждый следующий день они красят больше, чем в предыдущий на одно и тоже число метров. Известно, что за 1й и последний день в сумме они покрасили 20 метров забора. За ск-о дней был покрашен весь забор?
Решение
В данном случае мы видим все признаки арифметической прогрессии:
1) каждый следующий день они красят больше, чем в предыдущий на одно и тоже число метров, т.е.
а2=а1+d
a3=a2+d
a4=a3+d и т.д.
2) сумма членов арифметической прогрессии равна 100
примем
Sn=(a1+an)*n/2
a1+an=20
100=20*n/2
n=10
ответ: 10 дней
#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
![(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)](/tpl/images/0172/7524/775a9.png)
C учётом (-∞;3/2)U[2;6) получим ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ: ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC => 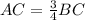
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
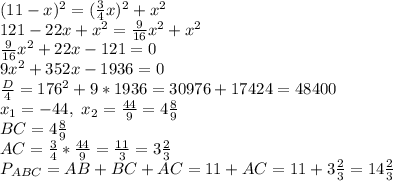
ответ: 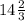
<> [ Здравствуйте, Kamo173286! ] <>
—
<> [ • ответные Объяснения: ] <>
—
В качестве изображения прилагаются цифры на основе системы нумерации Майя.
—
В нумерации Майя мы должны учитывать, что ноль представлен овалом. От 1 до 19 они следуют графическому шаблону, через точки и линии.
—
От 1 до 5: очки складываются, т. е.:
1: •
2: • •
3: • • •
4: • • • •
Начиная с 5, он представлен прямой: — .
—
С 6 по 9 используется прямая плюс количество точек, то есть: 6: прямая и одна точка, 7: прямая и две точки, 8: прямая и три точки, 9: прямая и 4 точки.
—
Это двадцатая система нумерации, поскольку она основана на числе 20. В зависимости от уровня числа ваш множитель будет 20:
—
Уровень 1: ×20 = = 1
Уровень 2: × 201 = 20
Уровень 3: × 202 = 400
—
<> [ С уважением, Hekady! ] <>
Первая труба пропускает х литров воды в минуту
вторая труба пропускает х+6 литров воды в минуту
Первая труба заполняет бак 360 литров за время 360/х минут
Вторая труба заполняет бак 360 литров за время 360/(х+6) минут = (360/х -10) минут
360/(х+6) = (360/х -10)
360*х = 360*(х+6)-10*х*(х+6)
360*6-10*х*(х+6)=0
х*х+6х-216=0
д=36+4*216=900
x=(-6±30)/2
x > 0
x = 12 литров/минуту
2)
ответ - за 10 дней
за первый день - a1 метров
за n день - а1 + (n-1)*d
за 1 и за n день - 2а1 + (n-1)*d = Z = 20
Sn = а1*n*+n(n-1)*d/2 = Z*n/2 = 100
n = 2*Sn/Z = 100 * 2 / 20 = 10 - это ответ