Доброї ночі.
Множину всіх значень, яких набуває залежна змінна (функція), називають областю значень функції.
Область значення функції y = f(x) позначають E(f) або E(y).
В завданні умова , що "а" деяке відмінне від нуля число. Нуль не належить проміжку [а; +∞), а це значить, що "а" набуває тільки додатних значень, і що "а" належить даному проміжку. Цій умові відповідає функція у=(х+4)^2+6, вітки параболи напрямлені вгору, вершина параболи в точці (-4; 6), тоді Е(у)=[6; +∞).
Відповідь. Г.
Для решти функцій:
А) у=|/x , E(y)=[0;+∞),
Б) у=3х-2, Е(у)=(-∞;+∞),
В) у=|х|, Е(у)=[0;+∞),
області значень цих функцій не відповідають умові завдання.
1) Неопределённость вида ∞/∞ . Предел частного многочленов при
х--> ∞ равен отношению старших коэффициентов, если многочлены равных степеней . Значит, в заданном примере в числитель можно записать любой многочлен второй степени со старшим коэффициентом, равным 2 .
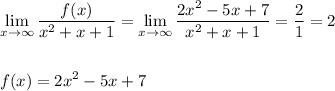
2) Неопределённость 0/0 . Многочлены раскладываются на множители , причём выделяется в обоих многочленах одинаковый множитель, который приводил к такой неопределённости . В данном примере это (х-1) . Затем он сокращается и неопределённость пропадает.
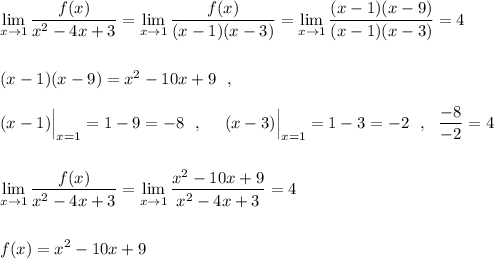
Смотри..................