Согласно определению противоположных чисел, два числа будут являться противоположными, если после прибавления одного числа к другому в результате получится ноль.
Для нахождения параметра а воспользуемся теоремой Виета.
Согласно этой теореме сумма корней данного уравнения x^2 + (a - 2)x + a - 6 = 0 равна -(а - 2).
Следовательно, для того, чтобы корни данного уравнения были противоположными числами необходимо, чтобы выполнялось условие:
-(а - 2) = 0,
откуда следует:
а = 2.
Проверим, имеет ли уравнение x^2 + (a - 2)x + a - 6 = 0 корни при а = 2.
Подставляя данное значение параметра а в уравнение, получаем:
x^2 + (2 - 2)x + 2 - 6 = 0;
x^2 - 4 = 0;
(х - 2) * (х + 2) = 0;
х1 = 2;
х2 = -2.
Таким образом, корни данного уравнения являются противоположными числами при а = 2.
ответ: при а = 2.
Здесь от каждой дроби берётся целая часть.
Значит, дроби меньше единицы здесь имеют целую часть, равную нулю:
![$\left[\frac{7}{10}\right]=0;\ \ \ \left[\frac{8}{10}\right]=0;\ \ \ \left[\frac{9}{10}\right]=0](/tpl/images/2010/2141/944b3.png)
Все остальные дроби (с числителями от 10 до 19)- каждая имеет целую часть, равную единице:![$\left[\frac{10}{10}\right]=\left[\frac{11}{10}\right]=\left[\frac{12}{10}\right]=\left[\frac{13}{10}\right]=\left[\frac{14}{10}\right]=\left[\frac{15}{10}\right]=\left[\frac{16}{10}\right]=\left[\frac{17}{10}\right]=\left[\frac{18}{10}\right]=\left[\frac{19}{10}\right]=1](/tpl/images/2010/2141/5a665.png)
Всего таких дробей 10 штук, что даст общую сумму всего примера, равную:
1 * 10 = 10
Или вот, полностью весь пример:![$\left[\frac{7}{10}\right]+\left[\frac{8}{10}\right]+\left[\frac{9}{10}\right]+\left[\frac{10}{10}\right]+\left[\frac{11}{10}\right]+\left[\frac{12}{10}\right]+\left[\frac{13}{10}\right]+\left[\frac{14}{10}\right]+\left[\frac{15}{10}\right]+\left[\frac{16}{10}\right]+\left[\frac{17}{10}\right]+\left[\frac{18}{10}\right]+\left[\frac{19}{10}\right]=](/tpl/images/2010/2141/0fa71.png)
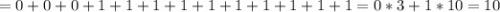
ответ: 10
P.S.
Целая часть находится делением нацело на 10
Например:
7 : 10 = 0 целых (и 7 в остатке)
10 : 10 = 1 целая (и 0 в остатке)
19 : 10 = 1 целая (и 9 в остатке)
Если бы был знаменатель посложнее, чем 10, то можно было бы делить уголком например. Ну, или на калькуляторе всегда можно поделить и увидеть целую часть дроби.
а) x²-x=0
x(x-1)=0
x=0; x=1
2) x²+5x+6=0
D=25-4*6=25-24=1
x1=(-5+1)/2=-2
x2=(-5-1)/2=-3
3) 5x²+8x-4=0
D=64-5*4*(-4)=64+80=144
x1=(-8+12)/10=0,4
x2=(-8-12)/10=-2
4) x²-6x+7=0
D=36-4*7=36-28=8
x=(6+√8)/2 или x=(6-√8)/2