Объяснение:
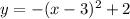
- Парабола ветвями вниз, смещена на (3; 2)
1) D(y) = R
2) E(y) = (-∞; 2]
3) неприрывная, не четная
4) Нули: y = 0, при x = -√2 + 3; x = √2 + 3
5) y > 0 при x ∈ (-√2+3; √2+3);
y < 0 при x ∈ (-∞; -√2+3) U (√2+3; +∞)
6) Возрастает на промежутке x ∈ (-∞; 3]
Убывает на промежутке x ∈ [3; +∞)
7) Ymax = 2
Система:
y < -(x - 3)² + 2
y > -1
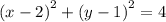
- не является графиком (уравнение окружности)
Система:
(x - 2)² + (y - 1)² < 4
x < 3
чтобы решить уравнение нужно привести всё к общему знаменателю
х 7 8
___ - =
х-2 х + 2 х² - 4
нижний знаменатель х² - 4 можно разложить по формуле разности квадрата. вы её наверняка проходили.
получится (х-2)(х+2)
всё уравнение имеет вид
х 7 8
___ - =
х-2 х + 2 (х-2)(х+2)
ну а теперь домножаем до одного знаменателя. в первом столбике умножим на (х+2), во втором на (х-2), а третий так и оставим.
получится:
х(х+2) - 7(х-2) - 8
= 0;
(х-2)(х+2)
когда раскроем скобки получится:
х² + 2х - 7х + 14 - 8
= 0;
(х-2)(х+2)
сверху получится х² - 5х + 6 = 0
находим через дискриминант. D = b² - 4ac;
D = 25 - 4*6 = 25-24 = 1;
х₁= -b + √D
= 5 + 1
2a 2
x₁ = 3;
х₂ = 5-1
___ = 2
2
всё уравнение имеет вид
(x-2)(x-3)
= 0;
(х-2)(х+2)
сократив дробь получим
х-3
___ = 0;
х + 2
т.к. делить на ноль нельзя, то х+2 ≠0
х ≠ -2
ответ: х∋(-∞;-2)(-2;+∞)
на самом деле это несложное уравнение, просто я пыталась как можно больше объяснить свои действия :)
Объяснение:
Если нужна система неравенств, то пишем уравнения.
Задача а)
1) у = -(х - 3)² + 2 - парабола
2) y ≥ - 1 - прямая
Находим границы Х решив уравнение.
3) - (х - 3)² + 2 = -1
4) -(х² - 6*х +9) + 3 = 0
5) -х² + 6*х - 6 = 0
Решаем квадратное уравнение.
D=12, √12 = 2√3.
Корни ... х1 = 3-√3 ≈ 1,27 и х2 = 3+√3 ≈ 4,73 -
3 -√3 ≤ Х ≤ 3 +√3 ответ
Задача б)
Пересечение окружности и прямой.
Уравнение окружности
1) (x - 2)² + (x - 1)² = 2² ≤ 4 - внутри окружности
2) 0 ≤ x ≤ 3 - левее прямой