1. Какая часть объема плавающего тела погружена в жидкость, если плотность тела в 3 раза меньше плотности жидкости?
1/3 часть объёма.
2. В каком случае на плавающую пробку действует бОльшая сила Архимеда - когда пробка плавает в воде или когда она плавает в керосине?
думаю на плавающий предмет действует одинаковая сила в любой жидкости и она равна весу предмета.
3. Чем объясняются огромные размеры воздушных шаров?
маленькой выталкивающей силой в газах
4. Почему воздушный шар надо заполнять газом, плотность которого меньше плотности окружающего воздуха?
чтобы создать подьёмную силу, которая равна разности между выталкивающей силой и весом шара
Объяснение:
Дано:
a = 0,1 м
q₁ = + 1·10⁻⁴ Кл
q₂ = - 1 ·10⁻⁴ Кл
_____________
E - ?
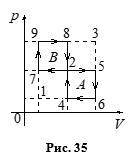
Сделаем чертеж. Проведем координатные оси через третью вершину треугольника.
Заметим, что по модулю заряды одинаковы:
q = |q₁| = |q₂|
Тогда, по модулю:
E₁ = E₂ = k·q / a² = 9·10⁹·1·10⁻⁴/0,01 = 90·10⁶ В/м или 90 МВ/м
Проекции векторов напряженности на оси:
Eₓ = E₁·cosα - E₂ = E₁·(cos α - 1) = E₁·(cos 60° - 1) =
= 90·(0,5- 1) = - 45 МВ/м
Eу = - E₁·sin α = - 90·√3/2 ≈ - 78 МВ/м
По теореме Пифагора:
E = √ ( Eₓ²+Ey²) = √( (-45)²+(-78)²) ≈ √8100 = 90 МВ/м
Объяснение:
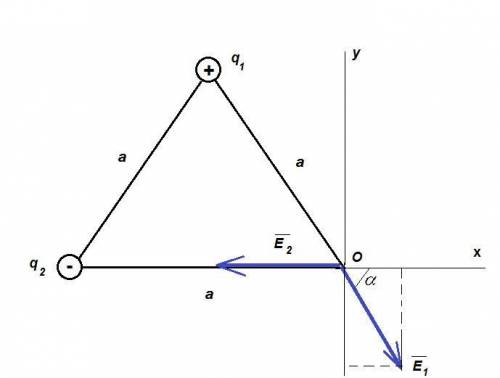
допустим для определенности что давление в точке 2 равно р, объем в точке 2 равен V
работа газа на обоих циклических участках равна площади квадрата и составляет A=Δp*ΔV
чтоб знать кпд надо вычислить поступление теплоты
для процесса А теплота поступает на участках 42 и 25
Q42=3/2*(p*V-(p-Δp)*V)=3/2*Δp*V
Q25=3/2*(p*(V+ΔV)-p*(V))=3/2*p*ΔV
для процесса В теплота поступает на участках 79 и 98
Q79=3/2*((p+Δp)*(V-ΔV)-(p)*(V-ΔV))=3/2*Δp*(V-ΔV)
Q98=3/2*((p+Δp)*(V)-(p+Δp)*(V-ΔV)=3/2*(p+Δp)*ΔV
теперь сравним
Q42+Q25=3/2*Δp*V+3/2*p*ΔV
Q79+Q98=3/2*Δp*(V-ΔV)+3/2*(p+Δp)*ΔV=3/2*Δp*V+3/2*p*ΔV
получилось что Q42+Q25=Q79+Q98
это значит что у обоих процессов не только одинаковая выполненая работа но и одинаковое подведенное тепло
это значит что кпд также одинаковы
кпд = работа / подведенное тепло