На расстоянии 10 см от левого конца стержня
Объяснение:
К концам стержня длиной 40 см и массой 10 кг подвесили грузы массой 40 и 10 кг. Где надо подпереть стержень, чтобы он находился в равновесии?
Дано:
L = 40 см = 0,40 м
m₁ = 40 кг; F₁ = m₁·g = 40·10 = 400 Н
m₂ = 10 кг; F₂ = m₂·g = 10·10 = 100 Н
m₃ = 10 кг; F₃ = m₃·g = 10·10 = 100 Н
____________________
x - ?
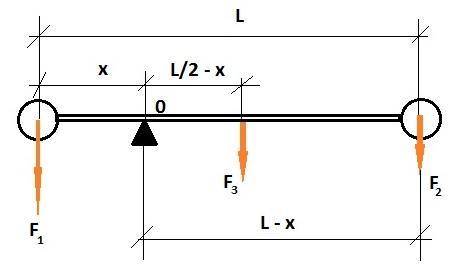
Сделаем чертеж.
Составим уравнение моментов:
F₁·x = F₂·(L-x)+F₃·(L/2-x)
400·x = 100·(0,40 - x) + 100·(0,20 - x)
400·x = 40 - 100· x + 20 - 100·x
600·x = 60
x = 60/600 = 0,10 м или 10 см
Дано: СИ Решение:
S = 90 км 90000 м v₁ / t + v₂ / t = S ⇒ t = S / v₁ + v₂ = 90000 м / (20 м / с)
v₁ = 20 м / с 15 м / с + (15 м / с) ≈ 2571 c ≈ 42.85 мин ≈ 0.7 ч
v₂ = 54 км / ч ответ: t ≈ 0.7 ч
t - ?