Медианы треугольника пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершины треугольника.
Пусть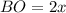 
см и 
см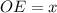, тогда 
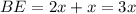, что по условию он равен 9 см.
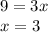
Следовательно,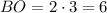 
см и 
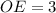см
Аналогично, пусть теперь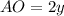 
см и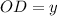 
, тогда 
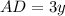и по условию равен 12 см
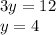
Таким образом,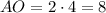 
см и 
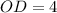см.
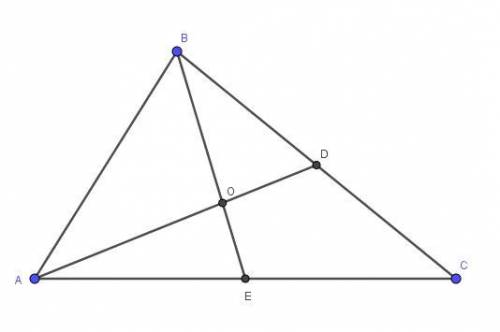
По условию медианы треугольника AD и BE взаимно перпендикулярны, следовательно
По теореме Пифагора из прямоугольного треугольника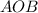 
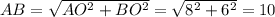см
По теореме Пифагора из прямоугольного треугольника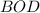 
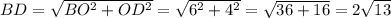см
Тогда 
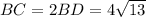см
Из прямоугольного треугольника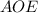 
по теореме Пифагора
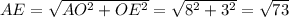см
Тогда 
см
ответ: 
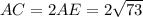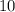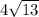см;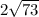 
см; 
см.
Формула вычисления стороны квадрата, зная описанный радиус: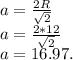 
Формула вычисления радиуса вписанной окружности в квадрат, зная его сторону:
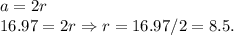
Вывод: Сторона квадрата равна: 16.97; радиус вписанной окружности — 8.5.
8.Формула вычисления радиуса описанной окружности, зная сторону правильного треугольника:
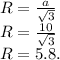
Длина круга равна:
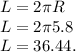
Не поняла, площадь какого круга надо найти, так что найду площади и вписанной, и описанной окружности.
Формула вычисления площади описанной окружности такова:
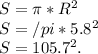
Формула вычисления площади вписанной окружности такова: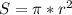 
Радиус вписанной окружности в правильный треугольник, мы найдём по стороне этого же треугольника:
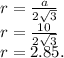
Площадь окружности равна:
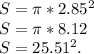
Формула вычисления стороны правильного треугольника, зная радиус описанной окружности:
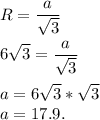
Радиус вписанной окружности равен:
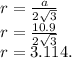
Площадь окружности равна:
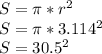
Дано: АВСЕ - трапеція, ВС=8 см, АЕ=12 см. МР - середня лінія. Знайти КТ.
ΔАВС; МК - середня лінія, МК=1/2 ВС=4 см
ΔАСЕ; КР - середня лінія; КР=1/2 АЕ=6 см
МР=МК+КР=10 см;
ΔВСЕ; ТР - середня лінія; ТР=1/2 ВС=4 см.
КТ=МР-МК-ТР=10-4-4=2 см.
Відповідь: 2 см.