Задача сводится к решению планиметрической задачи на отыскание радиуса круга, вписанного в осевое сечение конуса, т.к. осевое сечение - равнобедренный треугольник, боковые стороны которого — образующие конуса, а основание — его диаметр . Вписанный в этот треугольник круг - это круг, радиус которого равен радиусу шара.
поэтому чтобы найти радиус шара, достаточно найти радиус круга, вписанного в треугольник. он равен частному от деления площади треугольника на полупериметр треугольника. Если в треугольнике опустить высоту на основание, то она равна √(17²-8²) =√(25*9)=15/см/, площадь треугольника равна 15*8=120/см²/, а полупериметр (2*17+2*8)/2=17+8=25, искомый радиус 120/25=24/5=4.8/см/
Пусть дан равнобедренный треугольник АВС, АВ = ВС = 10, АС = 4.
Если провести отрезки через вершину, середину боковой стороны и середину основания треугольника, то получим равнобедренный треугольник ВДЕ с двумя сторонами ВЕ и ДЕ по 5 и третьей ВД, равной высоте Н исходного треугольника.
Находим Н = √(10² - (4/2)²) = √(100 - 4) = √96 = 4√6.
Высота треугольника ВДЕ из точки Е на ВД равна (4/2)/2 = 1.
Площадь ВДЕ = (1/2)*1*(4√6) = 2√6 кв.ед.
Отсюда получаем ответ, использовав формулу:
R = (abc)/(4S) = (5*5*4√6)/(4*2√6) = 25/2 = 12,5 ед.
ответ: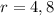 см.
см.
Объяснение:
Сечение конуса - равнобедренный треугольник, боковые стороны которого равны 17 см, а основание равно 8*2=16 см.
Радиус вписанной окружности в треугольник равен радиусу вписанного шара в конус.