Объяснение:
Решение дано на фото.
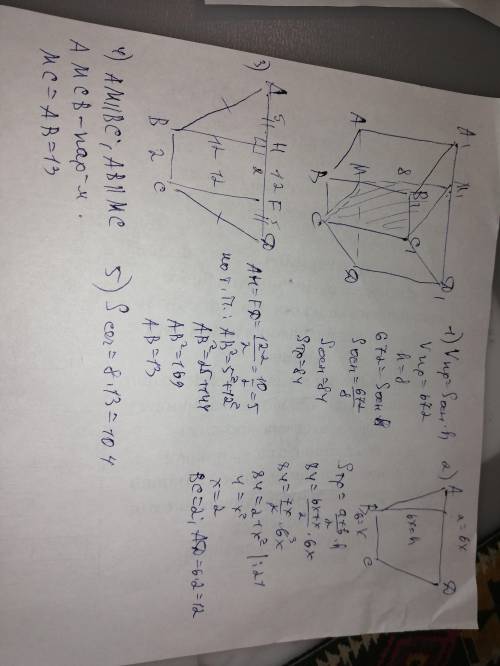
найдём диагонали прямоугольника по т. Пифагора
d1=d2=корень из4^2+6^2= корень из16+36= корень из52=2 корень из13
Отрезки, соединяющие середины сторон являются средними линиями треугольников и по свойству равны половине основания 2 корень из13:2= корень из13. Так как диагонали прямоугольника равны, то все стороны получившегося параллелограмма равны, значит он ромб. Площадь ромба можно найти как половину произведения диагоналей ромба. Диагонали ромба равны сторонам прямоугольника, поэтому S=1/2*4*6=12
Находим площадь основания призмы.
V = SoH, отсюда находим So = V/H = 672/8 = 84 кв.ед.
Примем ВС = х, а АД = 6х.
Проекция АВ на АД равна (6х - х)/2 = 2,5х.
Используем формулу площади трапеции.
So = ((6x + x)/2)*H, или 84 = 3,5х*6х = 21х².
Отсюда находим неизвестную х = √(84/21) = √4 = 2.
Теперь находим АВ = √((2,5х)² + (6х)²) = √(42,25х²) = 6,5х.
Длина АВ = 6,5*2 = 13.
Переходим к заданному сечению.
Это прямоугольник, основание равно АВ как параллельная секущая при параллельных прямых, высота равна высоте призмы.
ответ: Sсеч = 13*8 = 104 кв.ед.