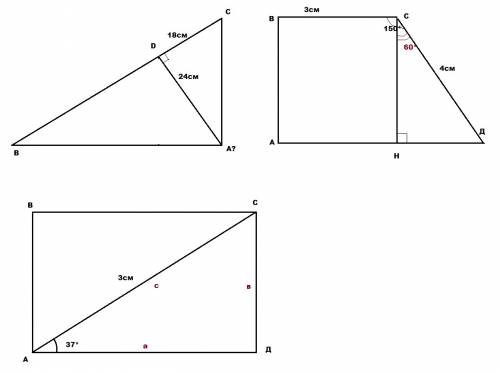
1) 1. рассмотрим АДС-прямоугольный (АД-высота) АД=24см ДС=18см . по тПифагора СА=sqrt24^2+18^2=30cm
2. из соотношения сторон и высоты к гипотенузе прямоугольного треугольника имеем
АС^2=CD*CB CB=AC^2 / CD CB=30^2 / 18= 50cm ДВ=50-18=32см
АВ^2 =DB*CB AB^2=50*32=1600cm^2 AB=40cm
можно было проще : египетский треугольник , соотношение сторон 3:4:5
у АВС АС=30см СВ=50см АС:АВ:СВ =3:4:5=30 :40:50 АВ= 40см
3. сos A -?????? cos90* =0
cosCBA= BA /BC cosBCA=CA/BC cosBAD=BD / BA cosDAC=DA/CA =24 /30=4/5
подставь длинну катета и гипотенузы и вычисли
2) АВСД- трапеция угА=угВ=90*, ВС=3см, СД=4см угВСД=150*
1)проведем СН-высота угВСН=СНА=90* угНСД=150*-90*=60* АН=3см
2)рассмотрим треугольник НСД-прямоугольный угСНД=90* угНСД=60* значт угНДС=30*
напротив угла 30* лежит сторона = 1/2 гипотенузы , отсюда СН=1/2СД =2см
по т Пифагора НД=sqrt (4^2-2^2)=2sqrt3 (2 корня из3)
3) Sтрап =( (a+b) /2 ) * h
S(ABCD) = (3+3+2sqrt3) / 2) *2 =(6+2sqrt3) cm^2
3) Sпрямоуг= а*в
пусть а=АД в=СД
рассмотримАСД-прямоугольный угД=90* САД=37* cos37*= a /c sin37*=b/c
a=3 cos37* b=3 sin37*
S= 3 cos37* * 3 sin37* = 9 * 1/2 sin(37*2)= 4.5 sin74*
Решение: Рассмотрим треугольник ACH: Так как CH - высота,то этот треугольник прямоугольный. Следовательно CH - катет и мы находим его по теореме Пифагора: CH = √6^²-4^² = √36-16 = √20 = 2√5
Я предлагаю рассмотреть треугольник ABC и найти x через CB(не знаю можно ли так,как я решил,но я запишу)
AB=4+x
CB=√AB²-AC² = √(4-x)²-6² = √x²-10x-20
Разбираем квадратичное уравнение:
x²-10x-20=0
D= 100+4*20=180 √D= 6√5
x_{12} = 5+-3√5
x2 - не подходит,так как получается отрицательным,поэтому BH = 5+3√5.
ответ: 5+3√5