ответ: 4; 8; 12; 16.
Объяснение:
Т. Фалеса: Если на одной из двух прямых отложить последовательно несколько равных между собой отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Задачу можно решать разными . Вот один из них.
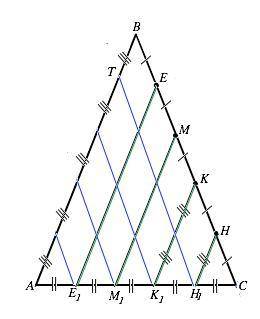
Пусть точки Е, М, К, Н делят сторону ВС на равные части, и ЕЕ1, ММ1, КК1 и НН1 параллельны АВ ( дано по условию). Тогда СН1=Н1К1=К1М1=М1Е1=Е1А.
По той же теореме Фалеса прямые, проведенные из точек Е1, М1, К1, Н1 параллельно ВС, делят АВ на равные 5 равных частей, каждая из которых равна 20:5=4, и каждый отрезок, проведенный параллельно АВ из Н, К, М, Е, – на равные части.
Тогда НН1 параллельна АВ и равна АВ/5, т.е. НН1=ВТ=4. Остальные отрезки пропорциональны НН1: КК1=2•НН1=2•4=8; ММ1=3•НН1=12; ЕЕ1=4•НН1=16.
Биссектриса прямого угла прямоугольного треугольника делит гипотенузу на отрезки длиной 3см 4см. Найдите радиус круга, вписанного в треугольник
Объяснение:
Пусть один катет а, другой катет b. . По т. о биссектрисе треугольника
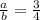, тогда а= 
.
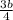По т. Пифагора а²+b²=(3+4)² ,( 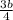)²+b²=49 ,
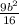+b²=49 , 9b²+16b²=49*16 , b²= 
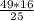, b=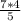
= 5,6 (см)
a=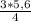 
=4,2 cм
S=1/2*Р*r . Найдем площадь прямоугольного треугольника
S=1/2*5,6*4,2=1/2*23,52 (см²) . Найдем периметр Р=16,8 см. Тогда
1/2*23,52=1/2*16,8*r , r= 23,52/16,8 , r=1,4 см
===============================
Теорема о биссектрисе треугольника " Биссектриса треугольника делит противоположную сторону на два отрезка, длины которых относятся так же, как длины соответствующих сторон."
Угол LTD = 44, TM - биссектриса, следовательно угол MTD = 44/2=22
Рассмотрим треугольник DMT
Угол DMT = 180-угол TDM- угол MYD= 180- 30-22=128
ответ: угол DMT = 128