О (0;9).
Объяснение:
1. Точка, лежащая на оси ординат, имеет абсциссу, равную нулю. Обозначим искомую точку О (0;у).
По условию О равноудалена от А(3;2) и В(7;6), тогда
ОА = ОВ.
ОА^2 = (3-0)^2 + (2-у)^2 = 9 + (2-у)^2.
ОВ^2 = (7-0)^2 + (6-у)^2 = 49 + (6-у)^2.
Составим и решим уравнение:
9 + (2-у)^2 = 49 + (6-у)^2
9 + 4 - 4у + у^2 = 49 + 36 -12у + у^2
13 - 4у = 85 -12у
12у - 4у = 85 - 13
8у = 72
у = 72 : 8
у = 9
О (0;9) - искомая точка.
Проверим полученный результат:
О (0;9), А(3;2) и В(7;6)
ОА^2 = (3-0)^2+(2-9)^2 = 9+49 = 58;
ОВ^2 = (7-0)^2+(6-9)^2 = 49+9 = 58.
ОА = ОВ - верно.
Из вершины прямого угла С проведена высота CD, равная 12 см. Катет ВС = 20 см. Найдите BD, АВ и cosА.
============================================================
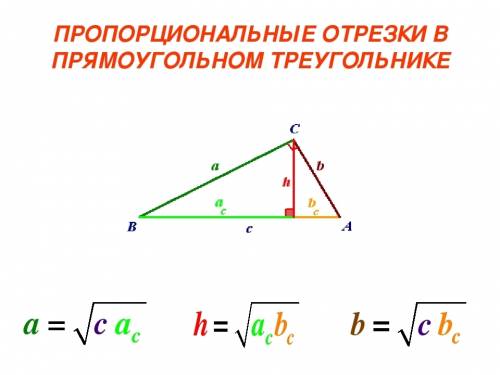
ΔABC - прямоугольный, CD⊥ABВ ΔBCD: по т. ПифагораBD² = BC² - CD² = 20² - 12² = 400 - 144 = 256BD = 16 смСвойства прямоугольного треугольника:1. Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.2. Катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.CD² = AD • BD ⇒ AD = CD²/ BD = 12²/16 = 144/16 = 9 смAB = AD + BD = 9 + 16 = 25 см▪Если в прямоугольном треугольнике высота опущена из вершины прямого угла на гипотенузу, то высота делит этот треугольник на 3 пары подобных прям. треугольников.Значит, ∠CAD = ∠BCD cos∠CAD = cos∠BCD = CD/BC = 12/20 = 6/10 = 0,6ОТВЕТ: BD = 16 см, АВ = 25 см, cosA = 0,6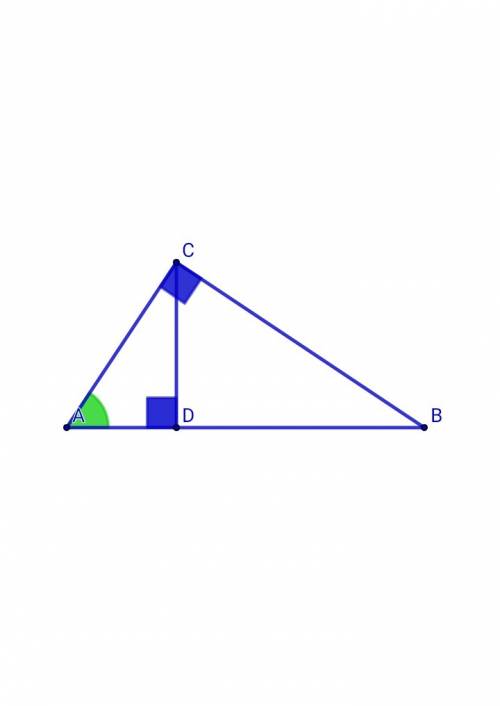
длина вектора AB+AD=8
Объяснение:
AB+AD=3+5=8