Дан квадрат ATMV .
T M
A V
1. Выполни параллельный перенос квадрата на вектор TV−→− .
2. Каким образом ещё можно получить тот же результат?
Поворотом на −180 градусов вокруг конечной точки данного вектора
Параллельным переносом на противоположный вектор
Поворотом на 180 градусов вокруг конечной точки данного вектора
Симметрией относительно прямой, на которой лежит данный вектор
Выполненный параллельный перенос на данный вектор — единственное возможное движение
Симметрией относительно конечной точки данного вектора
Поворотом на 180 градусов вокруг начальной точки данного вектора
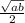, высота трапеции: h=2r=
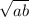=√8=2√2
Половина основания b/2=а*cos(30)=a*sqr(3)/2, b=a*sqr(3)
Известно, что:
R=a^2/sqr(4a^2-b^2)
Подставив значение b, получим: R=a
Отсюда: АВ=2 см
Во второй задаче центр вписанной окружности совпадает с точкой пересечения биссектрис, поскольку радиусы опущенные из центра в точки М, Т и Р, образуют пары равных прямоугольных треугольников (ВОМ и ВОТ и т.д.). Четырехугольник РОТС является квадратом, так как радиусы проведены в точки касания и перпендикулярны катетам. По условия диагональ этого квадрата равна корень из 8, следовательно сторона будет в корень из двух раз меньше, отсюда:
r=sqr(8/2)=2 Угол ТОР=90 град. Угол ТМР является вписанным, он измеряется половиной дуги, на которую опирается. Дуга составляет 90 градусов, так как ограничена точками Р и Т, а угол РСТ прямой. Следовательно угол ТМР=45 град.