S треугольника всегда = высота*основание к которому она проведена разделить это всё на два. (h*осн.)/2
1) высота - 6, основание 12, значит площадь - 12*6/2= 72/2=36 - Б
2)Если в треугольнике есть угол в 30 градусов, то сторона напротив него - в два раза меньше гипотенузы ( стороны напротив прямого=90 угла).
Тут гипотенуза = 12 значит сторона напротив угла равна 12/2 = 6. Чтобы найти вторую сторону используем теорему Пифагора.
a^2+b^2=c^2
где а и б - стороны, а с - гипотенуза. Подставим известное...
6^2+b^2=12^2
36+B^2=144
b^2=144-36
b^2=108
b = 
Площадь треугольника здесь - 6* /2 = 3*
/2 = 3* =18
=18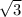 -в
-в
3)Опустим высоту. Найдём её тоже через свойство угла в 30 градусов и теорему пифагора. 16-4=12 значит высота 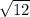 . в итоге.
. в итоге.
площадь=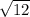 *6=6
*6=6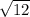 =12
=12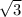 - в
- в
4)Наименьшая высота будет опущена к самой большой стороне, запомни. Опустим ее к стороне 20. Через формулы ( набери в инете среднее геометрическое, долго оформлять очень ) найдём, что x=12,8 - кусочек, которой получается в результате деления высотой стороны двадцать, который ближе к стороне 16. Аналогично найдём и кусочек, ближний к стороне 12. y=7,2. Высота равна корню произведения xy= 9,6 - высота - г
пусть ad> bc , тогда острые углы равные 75 и 15 гр лежат при оснований ad , положим что y,w середины сторон ab и cd соответственно , тогда yw средняя линия трапеции , значит ad+bc=2yw из условия мы знаем что yw равна либо 15 либо 7 , положим что ab и cd пересекаются в точке e , тогда aed=180-(75+15)=90 , положим также что z,x это середины сторон основании bc,ad соотвественно , пусть n точка пересечения yw и zx , тогда по замечательному свойству трапеции точки e,z,x лежат на одной прямой , учитывая что угол aed прямой , получаем что ax=ex=ad/2 , ez=bz=bc/2 , но так как ex=ez+zx откуда окончательно получаем две системы
{ad-bc=2*7
{ad+bc=2*15
или
{ad-bc=2*15
{ad+bc=2*7
подходит решение первой системы , так как они положительны , складывая получаем ad=22 , bc=8 , значит ответ bc=8.