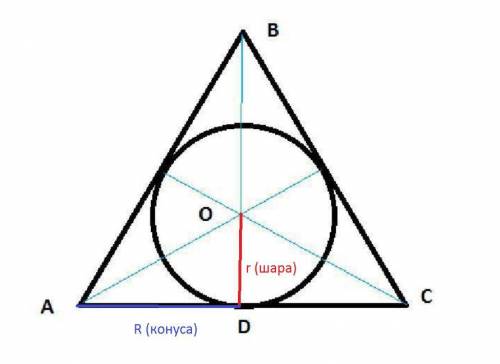
Осевое сечение конуса – равнобедренный треугольник АВС.
АВ=ВС – образующие.
BD– высота конуса, а также высота, медиана и биссектриса равнобедренного треугольника.
О–центр вписанной в треугольник АВС окружности и центр вписанного в конус шара.
ОD=r .
AD=R .
Из прямоугольного треугольника
tg∠OAD = tg(α/2) = r/R . Отсюда r = Rtg(α/2).
ОА– биссектриса угла ВAD, так как центр вписанной в треугольник окружности– точка пересечения биссектрис.
Высота конуса H = R/tg(α/2).
V(шара) = (4/3)πr³ = (4/3)πR³tg³(α/2).
V(конуса)=(1/3)S(осн)·H=(1/3)·πR²·R/tg(α/2) = (1/3)·πR³/tg(α/2).
Разделим V(конуса) на V(шара).
V(конуса) / V(шара) = ( (1/3)·πR³/tg(α/2)) / ((4/3)πR³tg³(α/2)) = 4tg³(α/2)tgα.
ответ: V(конуса) = V(шара) / (4tg³(α/2)tgα).
в данном случае все очень просто. Сечение строится так - через середину АС и ребро DB проводится плоскость. Это будет прямоугольный треугольник с катетом 2*корень(2) и гипотенузой 6. Второй катет равен 2*корень(7), а площадь 2*корень(14).
Необходимые пояснения.
В основании лежит прямоугольный равнобедренный треугольник, середина АС это центр описанной окружности. Поэтому вершина пирамиды D проектируется именно туда, поскольку она равноудалена от вершин (значит и проекция её равноудалена от вершин). Поэтому плоскость АСD перпендикулярна плоскости АВС. Если М - середина АС, то DM и ВМ - медианы в равнобедренных теругольниках, то есть они перпендикулярны АС, то есть угол между ними - это двугранный угол между перпендикулярными плоскостями :))). ВМ = 4*корень(2)/2 = 2*корень(2). А боковое ребро задано. Отсюда находим DM.