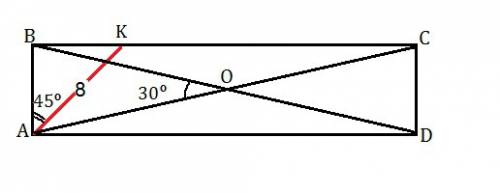
В прямоугольнике ABCD проведена биссектриса угла A до пересечения со стороной BC в точке K. Отрезок AK=8 см, угол между диагоналями прямоугольника равен 30°. Найдите стороны и площадь прямоугольника ABCD.
Обозначим точку пересечения диагоналей О.
Диагонали прямоугольника равны и точкой пересечения делятся пополам.
∆АОВ и ∆COD - равнобедренные, углы при АВ и CD равны по (180°-30°):2=75°⇒
в ∆ АВС ∠BСA=90°-75°=15°
∆ АВК - прямоугольный с острым углом ВАК=45°⇒
∠ВКА=45° ⇒ ∆ АВК равнобедренный.
АВ=АК*sin45°=(8*√2)/2=4√2 см
В ∆ АВС по т.синусов
АВ:sin15°=BC:sin75°
По таблице синусов
sin 15° =0,2588
sin75°=0,9659
4√2:0,2588=ВС:0,9659⇒
ВС=21,1127 см
S=AB•ВС=4√2•21,1127≈ 119,426 см²
------
Как вариант:
Найти из прямоугольного ∆ АВС диагональ АС:
АС=АВ:sin 15º=(4√2):0,2588
Площадь выпуклого четырехугольника равна половине произведения его диагоналей на синус угла между ними.
S=0,5•d₁•d₂•sinφ , где
d₁ и d₂ – диагонали, φ – любой из четырёх углов между ними/
Тогда S=0,5•{4√2):0,2588}²•0,5=≈ 119,426 см²
1. внутренняя
2.на плоскости равноудалённых от одной точки называемой центром окружности.
3.плоская,замкнутая или кривая все точки которой одинаково удалена от центра.
4.отрезок который соединяет две точки на окружности длина такого отрезка равна 2-м радиусам.
5.отрезок, соединяющий две точки кривой.
6.делит хорду пополам
7.прямая пересекающаяся окружность
8. касательная к окружности перпендикулярна к радиусу проведенная точку касания
9.если она касается всех сторон,а центр внутри окружности.
10. окружность треугольника касающаяся всех его сторон.
11. называется окружность, к которой является одна из сторон треугольника.
12. является точкой середины перпендикуляров к сторонам треугольника.