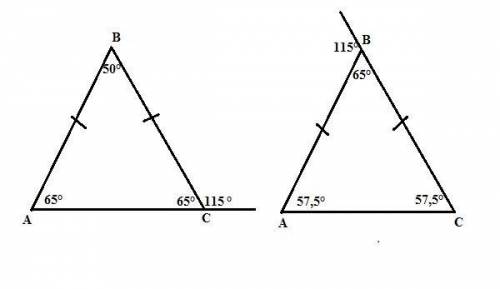
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
ответ: 12 см
Объяснение: Бонус от палаточника Хайяма:
Если мельницу, баню, роскошный дворец
Получает в подарок дурак и подлец,
А достойный идет в кабалу из-за хлеба,
Я плевал на твою справедливость, Творец!
Если в окружность вписан треугольник, то отношение стороны, противолежащей углу к синусу этого угла равно диаметру.
То есть
a: sina = 2R
Отсюда, а = 2Rsin30 = 2R*0,5 = R
a = 12 см
ответ: а = 12 см