Даны координаты вершин . ABC  1) В декартовой прямоугольной системе координат построить тре- угольник - id1413670020201127 от Змей19 27.11.2020 15:21

Question

Геометрия: Даны координаты вершин . ABC  1) В декартовой прямоугольной системе координат построить тре- угольник ABC 2) Написать каноническое и общее уравнения прямой АВ, найти ее угловой коэффициент. 3) Написать каноническое и общее уравнения прямой АС, найти ее угловой коэффициент 4) Найти внутренний угол А в градусах. 5) Написать общее уравнение высоты CD и найти ее длину. 6) Написать общее уравнение медианы СЕ. 7) Найти координаты точки пересечения высот треугольника АВС. На чертеже построить точку пересечения

Змей19 · Accepted Answer

CO = CD/2 = 12√3/2 = 6√3 см (диагонали ромба точкой пересечения делятся пополам)

AO = AB/2 = 12/2 = 6 см

Рассмотрим Δ ACO - прямоугольный: CO = 6√3 см, AO = 6 см, AC - ?

По теореме Пифагора

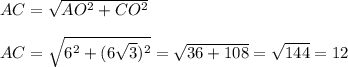
$AC = \sqrt{AO^2+CO^2} \\\\AC=\sqrt{6^2+(6\sqrt{3})^2 } =\sqrt{36+108} =\sqrt{144} =12$

Теорема: в прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы

==> ∠C = 30°

∠A = 90 - 30 = 60° (сумма острых углов в прямоугольном треугольнике равна 90°)

∠ACO = ∠OCB = 30° (диагонали ромба делят углы пополам)

∠ACB = 30 * 2 = 60°

∠ACB = ∠ADB = 60° (в ромбе противоположные углы равны)

∠CAB = ∠DAB = 60° (диагонали ромба делят углы пополам)

∠CAD = 60 * 2 = 120°

∠CAD = ∠CBD = 120° (диагонали ромба делят углы пополам)

ответ: ∠ACB = ∠ADB = 60°, ∠CAD = ∠CBD = 120°
Диагонали ромба равны 12 см и 12 корень 3 , найдите углы ромба

Диагонали ромба равны 12 см и 12 корень 3 , найдите углы ромба

MOGZ ответил