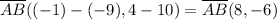 ;
; от точки A
от точки A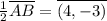 ;
; в обе возможные стороны
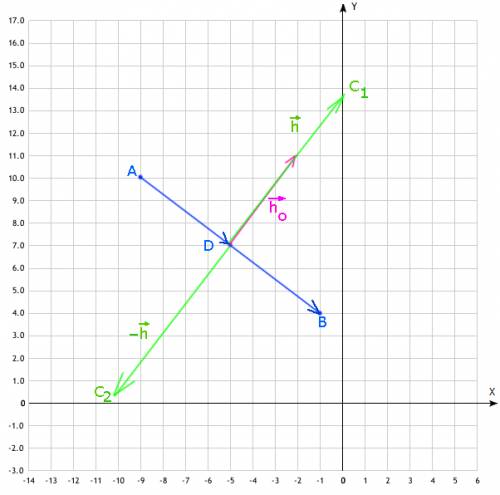
в обе возможные стороны перпендикулярен вектору основания
перпендикулярен вектору основания  , а значит его проекции накрест-пропорциональны с противоположным знаком:
, а значит его проекции накрест-пропорциональны с противоположным знаком: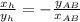 , что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:
, что непосредственно следует из скалярного произведения, поскольку для перпендикулярных векторов должно выполняться:  (II) ;
(II) ; пропорционален вектору
пропорционален вектору  , поскольку для вектора
, поскольку для вектора  выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора
выполняется и равенство (I) и равенство (II) осталось лишь найти масштаб вектора  ;
; имеет длину
имеет длину 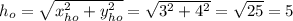 ;
;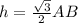 , т.к
, т.к 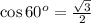 ;
;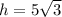 , а стало быть
, а стало быть  ;
;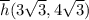 .
.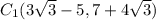 /// примечание:
/// примечание: 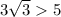 ;
;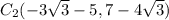 /// примечание:
/// примечание: 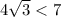 .
.
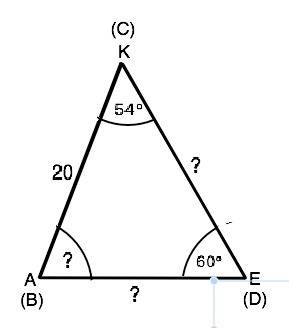
Для начала найдем неизвестные угол и стороны ∆ АКЕ. Сумма углов треугольника 180° => угол КАЕ=180°-(54°+60°=66°
По т.синусов АЕ=АК•sin54°/sin60°. KE=AK•sin66°/sin60°
sin60°=0.8660; sin54°= 0.8090; sin66°=0.9135
AE=20•0,8090/0,8660=18,683≈18,7 см; KE=20•0,9135/0,8660=21,097≈ 21,1 см
Стороны и углы треугольника ВСD имеют те же значения, что и соответствующие углы и стороны ∆ АКЕ, но в условии не указано, какие именно элементы двух треугольников равны. Если в ∆ ВСD сторона ВС=АК, и ∠D=∠Е, то ∠В=∠А=66°,∠С=∠К=54°, ВС=20 см, ВD=AE≈18,7= см, CD=KE≈21,1 см
АВСS-прав пирамида, в основании АВС-прав треугольник, SH-апофема, АН- высота, медиана, биссектриса. угSHA=45*,SO-высота пирамиды, О-ортоцентр тр-ка АВС
1)рассмотрим тр-к SOH -прямоугольный, уг SHO=45*, следовательно SO=OH=6cm
поскольку АН -медиана, О - ортоцентр, то АО=2ОН=12см, а АВ=18см
2) рассмотрим тр-к АНС-прямоуг, (АН-высота , медиана, биссектр) ,угАНС=90*, НСА=60*,САН=30* , НС=1/2АС=а, АН=18см
по т.пифагора СА^2=AH^2+HC^2 (2a)^2= 18^2+a^2 4a^2-a^2=324 a^2=108 a=6sqrt3 2a=12sqrt3
AC=12sqrt3