На сколько я понял требуется решить только первую задачу.
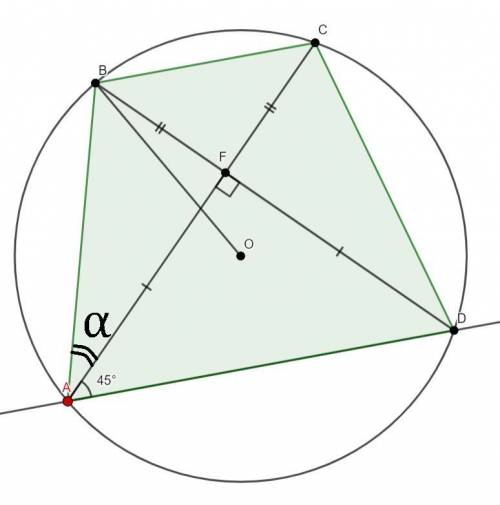
Дана трапеция ABCD, AB=CD=7√2 см; AC⊥BD.
Найти радиус описанной около ABCD.
Пусть AC∩BD=F и пусть ∠FAB=α.
Вокруг равнобедренной трапеции всегда можно описать окружность!
ΔABD=ΔDCA по двум сторонам и углу между ними (AB=DC; AD - общая; ∠BAD=∠CDA), поэтому ∠ADB=∠DAC, как углы лежащий напротив равных сторон в равных треугольниках.
В ΔAFD:
∠AFD=90°; ∠FAD=∠FDA=(180°-∠AFD):2=90°:2=45°. Таким образом ΔAFD - равнобедренный прямоугольны, AF=DF.
В прямоугольном ΔAFB:
AF=AB·cosα=7√2·cosα см
BF=AB·sinα=7√2·sinα см
В ΔABD:
BD=BF+FD=BF+AF=7√2·(sinα+cosα) см
∠BAD=α+45°
Вокруг ΔABD описана таже окружность, что и вокруг трапеции.
По теореме синусов: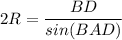 
, где R - радиус описанной.
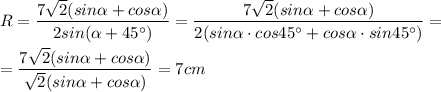
ответ: 7 см.
Дано: ΔABC - равнобедренный, АВ=ВС, Sabc= 192 см², АС=АВ+4, окружность, впис. в ΔАВС, OR - радиус, OR= 6 см
Найти: АВ, ВС, АС.
Решение.
Пусть АВ=ВС= х см. По условию основание на 4 см больше, чем боковая сторона, значит, АС= х+4.
Площадь треугольника равна произведению полупериметра треугольника на радиус вписанной окружности.
S= p•r, где S - площадь треугольника, p - его полупериметр, r - радиус вписанной окружности.
Находим периметр ΔАВС.
Р= АВ+ВС+АС= х+х+х+4= 3х+4.
Полупериметр равен соответственно р= (3х+4)/2.
S= p•r;
192= (3x+4)/2 •6;
192= (3х+4)•3;
192= 9х+12;
9х= 192–12;
9х= 180;
х= 20 (см)
Значит, АВ=ВС= 20 см, АС= х+4= 20+4= 24 см.
ответ: 20 см, 20 см, 24 см.
Рисунок фактически здесь вообще не нужен, однако, если Вам так легче это представить...