Сначало найдём угол D:
Сумма углов треугольника равна 180°
=> ∠D = 180 - (31 + 69) = 80°
Против большего угла лежит большая сторона.
Против меньшего угла лежит меньшая сторона.
∠D - наибольший угол => СЕ - наибольшая сторона.
∠Е - средний угол => CD - средняя сторона.
∠С - наименьший угол => ED - наименьшая сторона.
1) неверно, так как DE < CD (DE - наименьшая, а CD - средняя)
2) неверно, так как CD < CE (CD - средняя, а СЕ - наибольшая)
3) верно (CE - наибольшая, а DE - наименьшая)
4) неверно, так как DE < CE (DE - наименьшая, а СЕ - наибольшая)
ответ: 3)
ответ: обратная теорема - теорема, в которой условием является заключение, а заключением – условие данной теоремы. например, теоремы: "если два угла треугольника равны, то их биссектрисы равны" и "если две биссектрисы треугольника равны, то соответствующие им углы равны" — являются обратными друг другу.
обратная теорема, теорема, условием которой служит заключение исходной теоремы, а заключением — условие.
например:
теорема:
у равнобедренного треугольника углы при основании равны
обратная:
если в треугольнике углы при основании равны, то этот треугольник равнобедренный
теорема:
в треугольнике против большей стороны лежит больший угол
обратная:
в треугольнике против большего угла лежит большая сторона
теорема:
прямоугольник - параллелограмм, у которого равны диагонали.
обратная:
параллелограмм с равными диагоналями является прямоугольником.
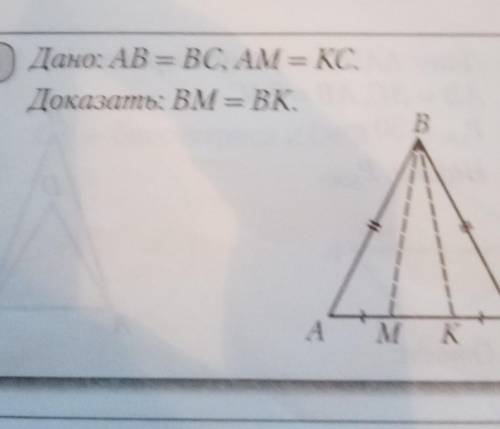
АВ=ВС значит ∆АВС равнобедренный
<А=<С
∆АВМ=∆СВК;(АВ=ВС;АМ=КС;<А=<С)
значит ВМ=ВК