1) РΔг = 45 ⇒ сторона аΔ = 45:3 = 15 см
2) сторона правильного многоугольника и радиус описанной окружности связаны между собой соотношением: а = 2Rsin(π/n), где n - число сторон ⇒ а3 = 2Rsin60 ⇒ R = 5√3
3) Тогда для правильного четырехугольника а4 = 2Rsin45 = 2·5√3·√2/2 = 5√6
ответ: а4 = 5√6
1)
Объяснение:
1) Все диаметры окружности равны между собой.
Верно.
Диаметр в два раза больше радиуса, а все радиусы окружности равны.
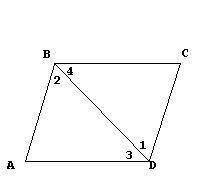
2) Диагональ трапеции делит ее на два равных треугольника.
Неверно.
Диагональ параллелограмма делит его на два равных треугольника, в трапеции эти треугольники очевидно не равны:
для ΔАВС и ΔADC АС - общая сторона, ∠1 = ∠2 как накрест лежащие при пересечении AD║ВС и секущей АС, но AD ≠ ВС.
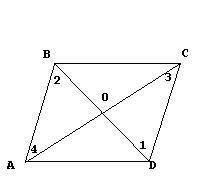
3) Площадь любого параллелограмма равна произведению длин его сторон.
Неверно.
Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
Если периметр правильного треугольника равен 45см, то сторона равна 15см.
Нати радиус окружности. R = a/V3 = 15/V3 = 5*V3см
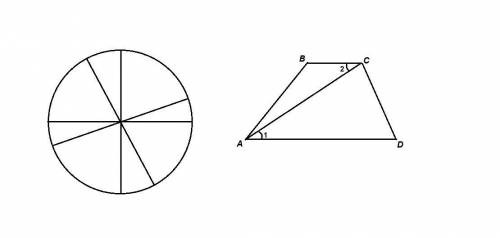
Для правильного восьмиугольника: 360:8 = 45 градусов - центральный угол
По теореме косинусов найти сторону правильного восьмиугольника.
a^2 = 75 + 75 - 2*75*cos45
a^2 = 150 - 75*V2 = 75(2 - V2)
a = sqrt(75*(2 - V2)) = 5*sqrt(6 - 3V2)