Треугольники АВС и АВD подобны по двум углам: <A у них общий, а <B=<C, так как <C=0,5 градусной меры дуги BD,как вписанный а <ABD=0,5 градусной меры дуги BD как угол между касательной и хордой BD. Из подобия имеем: АВ/АС=BD/BC=3/4. Следовательно, можем сказать, что АВ=3х, а АС=4х. Тогда по теореме косинусов из треугольника АВС имеем: ВС²=АВ²+АС² - 2*АВ*АС*CosA или 16=9х²+16х²-2*12х²*(7/8) => 16=4х². х=2. АВ=6, АС=8. По теореме о касательной и секущей АВ²=АС*AD => AD=36/8, DC=AC-AD = 7/2 =3,5. Площадь треугольника BCD по Герону при полупериметре р=5,25:
Sbcd = √(5,25*1,25*2,25*1,75)≈ 5,08.
R=a*b*c/4S или R = 3*4*3,5/(4*5,08) = 2,067.
ответ: АВ=6, R=2,067.
Объяснение:
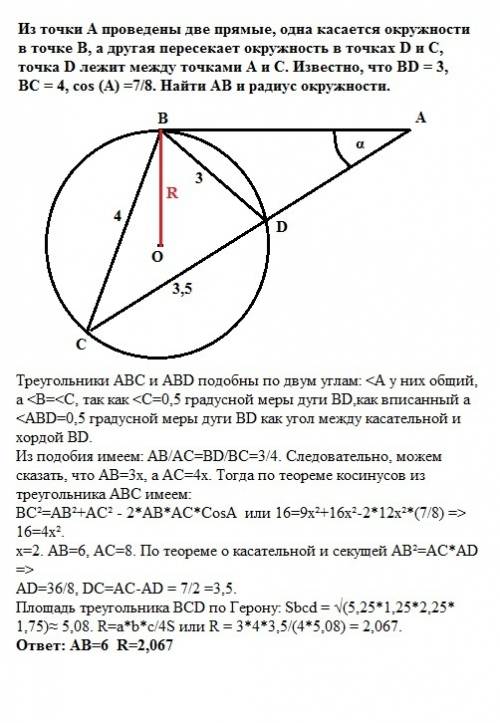
1кл=1см
1) треугольник ∆АВС
Площадь треугольника равна половине произведения основания на высоту опущенную на это основание.
ВК- высота
S1=АС*ВК/2=6*5/2=15см² площадь треугольника ∆АВС
ответ: площадь треугольника ∆АВС равна 15см²
2) параллелограм КРМО.
РН-высота
S2=PH*OM=5*5=25 см² площадь параллелограма.
ответ: 25см²
3) ромб АВСD
AС и ВD диагонали ромба
Площадь ромба равна половине произведения двух диагоналей
S3=АС*BD/2=4*6/2=24/2=12см² площадь ромба.
ответ: 12см²
4) ∆LMN
∆LMN- прямоугольный.
Площадь прямоугольного треугольника равна половине произведения двух катетов.
S4=LM*MN/2=3*5/2=7,5см² площадь треугольника ∆LMN
ответ: 7,5см²
5) трапеция ABCD.
Площадь трапеции равна произведению средней линии трапеции на высоту.
ВК- высота трапеции.
S4=BK*(BC+AD)/2
S4=3*(4+8)/2=3*12/2=36/2=18см² площадь трапеции
ответ:18см²